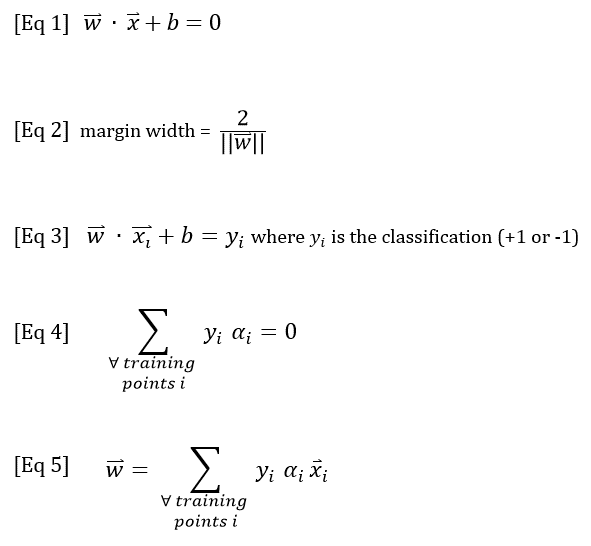Lab 8: Support Vector Machines

From 6.034 Wiki

(Difference between revisions)

Jump to: navigation, search

Current revision

1 The More, the Merrier
2 The Support Vector Machine
3 Equation Reference
4 Part 1: Vector Math
5 Part 2: Using the SVM Boundary Equations
6 Part 3: Supportiveness
- 6.1 Supportiveness is never negative, and is 0 for non-support-vectors
- 6.2 Supportiveness values must be internally consistent
7 Part 4: Evaluating Accuracy
8 Part 5: Training a support vector machine
9 Part 6: Multiple Choice Questions about SVM Training
10 If you want to do more...
11 API
12 Survey

This lab is due by Thursday, November 12 at 10:00pm.

Before working on the lab, you will need to get the code. You can...

Use Git on your computer: git clone username@athena.dialup.mit.edu:/mit/6.034/www/labs/fall2020/lab8

Use Git on Athena: git clone /mit/6.034/www/labs/fall2020/lab8

Download it as a ZIP file: http://web.mit.edu/6.034/www/labs/fall2020/lab8/lab8.zip

View the files individually: http://web.mit.edu/6.034/www/labs/fall2020/lab8/

All of your answers belong in the main file lab8.py. To submit your lab to the test server, you will need to download your key.py file and put it in either your lab8 directory or its parent directory. You can also view all of your lab submissions and grades here.

The More, the Merrier

So far in 6.034, we've discussed a few different supervised machine learning algorithms:

k-nearest neighbors (kNN), which classify points based on which training points are nearby
identification trees (ID trees), which classify points using a tree-based exploration
neural networks (NN), which classify points by iteratively applying small, primitive mathematical operations on features

The Support Vector Machine (SVM) is yet another supervised machine learning algorithm. An SVM classifies a point by, conceptually, comparing it against the most "important" training points, which are called the support vectors. The support vectors of classification C which are most similar to x win the vote, and x is consequently classified as C. In this way, an SVM can be likened to doing nearest neighbors comparison.

Importantly, SVMs can be very robust, as the principle paradigm of the SVM algorithm is that the classifier always maximizes the margin between the differently-classified data points. Visually, if you imagine drawing a decision boundary in a plane to separate two different classifications of data, an SVM will always position the decision boundary in such a way as to maximize the distance to the closest training points.

You might find the following diagram (inspired by Robert McIntyre's notes) helpful as a visual reference throughout this lab:

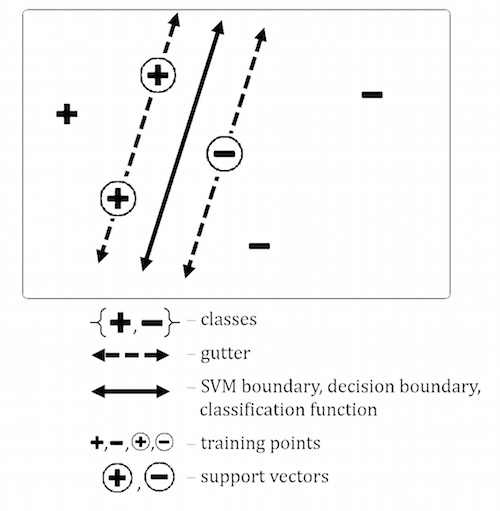
The Support Vector Machine

An SVM is a numeric classifier. That means that all of the features of the data must be numeric, not symbolic. Furthermore, in this class, we'll assume that the SVM is a binary classifier: that is, it classifies points as one of two classifications. We'll typically call the classifications "+" and "-".

A trained SVM is defined by two values:

A normal vector w (also called the weight vector), which solely determines the shape and direction of the decision boundary.
A scalar offset b, which solely determines the position of the decision boundary with respect to the origin.

A trained SVM can then classify a point x by computing w · x + b. If this value is positive, x is classified as +; otherwise, x is classified as -.

The decision boundary is coerced by support vectors, so called because these vectors (data points) support the boundary: if any of these points are moved or eliminated, the decision boundary changes! All support vectors lie on a gutter, which can be thought of as a line running parallel to the decision boundary. There are two gutters: one gutter hosts positive support vectors, and the other, negative support vectors.

Note that, though a support vector is always on a gutter, it's not necessarily true that every data point on a gutter is a support vector.

Equation Reference

Below are the five principle SVM equations, as taught in lecture and recitation. Equations 1-3 define the decision boundary and the margin width, while Equations 4 and 5 can be used to calculate the alpha (supportiveness) values for the training points.

For more information about how to apply these equations, see:

Part 1: Vector Math

We'll start with some basic functions for manipulating vectors. For now, we will represent an n-dimensional vector as a list or tuple of n coordinates. dot_product should compute the dot product of two vectors, while norm computes the length of a vector. Implement both functions.

(If these look familiar, it's probably because you saw them on Lab 5. Feel free to copy your implementations from your lab5.py.)

def dot_product(u, v):

def norm(v):

Later, when you need to actually manipulate vectors, note that we have also provided methods for adding two vectors (vector_add) and for multiplying a scalar by a vector (scalar_mult). (See the API, below.)

Part 2: Using the SVM Boundary Equations

Equations 1 and 3 above describe how certain data points must interact with the SVM decision boundary and gutters.

We will start by leveraging Equation 1 to classify a point with a given SVM (ignoring the point's actual classification, if any). Per Equation 1,

a point's classification is +1 when w·x + b > 0
a point's classification is -1 when w·x + b < 0

If w·x + b = 0, the point lies on the decision boundary, so its classification is ambiguous.

First, implement positiveness(svm, point) which evaluates the expression w·x + b to calculate how positive a point is. The first argument, svm, is a SupportVectorMachine object, and point is a Point object.

def positiveness(svm, point):

Next, classify a point as +1 or -1. If the point lies on the boundary, return 0.

def classify(svm, point):

Next, use the SVM's current decision boundary to calculate its margin width (Equation 2):

def margin_width(svm):

Finally, we will check that the gutter constraint is satisfied with the SVM's current support vectors and boundary. The gutter constraint imposes two restrictions simultaneously:

The positiveness of a positive support vector must be +1, and the positiveness of a negative support vector must be -1.
No training point may lie strictly between the gutters. That is, each training point should have a positiveness value indicating that it either lies on a gutter or outside the margin.

Note that the gutter constraint does not check whether points are classified correctly: it just checks that the gutter constraint holds for the current assigned classification of a point.

Implement check_gutter_constraint, which should return a set (not a list) of the training points that violate one or both conditions:

def check_gutter_constraint(svm):

Part 3: Supportiveness

To train a support vector machine, every training point is assigned a supportiveness value (also known as an alpha value, or a Lagrange multiplier), representing how important the point is in determining (or "supporting") the decision boundary. The supportiveness values must satisfy a number of conditions, which we will explore below.

Supportiveness is never negative, and is 0 for non-support-vectors

First, implement check_alpha_signs to ensure that each point's supportiveness value satisfies two conditions:

Each training point should have a non-negative supportiveness.
Each support vector should have positive supportiveness, while each non-support vector should have a supportiveness of 0.

Note: each point's supportiveness value can be accessed a property of the point. See the API for more information.

This function, like check_gutter_constraint above, should return a set of the training points that violate either of the supportiveness conditions.

def check_alpha_signs(svm):

Supportiveness values must be internally consistent

Implement check_alpha_equations to check that the SVM's supportiveness values are:

consistent with its boundary equation, according to Equation 4, and
consistent with the classifications of its training points, according to Equation 5.

This function should return True if both Equations 4 and 5 are satisfied, otherwise False. Remember the vector_add and scalar_mult helper functions are given to you in the API if you'd like to use them in your implementation.

def check_alpha_equations(svm):

Part 4: Evaluating Accuracy

Once a support vector machine has been trained -- or even while it is being trained -- we want to know how well it has classified the training data. Write a function that checks whether the training points were classified correctly and returns a set containing the training points that were misclassified, if any. Hint: You might find it helpful to use a function that you perviously defined.

def misclassified_training_points(svm):

Part 5: Training a support vector machine

So far, we have seen how to calculate the final parameters of an SVM (given the decision boundary), and we've used the equations to assess how well an SVM has been trained, but we haven't actually attempted to train an SVM.

In practice, training an SVM is a hill-climbing problem in alpha-space using the Lagrangian. There's a bit of math involved, and the equations are typically solved using Sequential Minimal Optimization (SMO), a type of quadratic programming (which is similar to linear programming, but more complicated).

...but if that sounds scary, don't worry -- we've provided code to do most of it for you!

What `train_svm` does

In train_svm.py, we've provided some SVM-solving code, originally written by past 6.034 student Crystal Pan. Here is a very high-level pseudocode overview of what the function train_svm (in train_svm.py) does:

while (alphas are still changing) and (iteration < max_iter):
    for i in training_points:
        for j in training_points:
            Update i.alpha and j.alpha using SMO to minimize ||w|| (i.e. maximize the margin width)

        Update the SVM's w, b, and support_vectors (using a function you'll write)
        Update the displayed graph using display_svm.py

Print the final decision boundary and number of misclassified points
Return the trained SVM

We've also provided visualization code in display_svm.py, originally written by past 6.034 student Kelly Shen. This code is automatically called by train_svm, although you can adjust the parameters (or disable graphing) by calling train_svm with additional arguments.

Note that the visualization requires the Python module Matplotlib. If you don't currently have Matplotlib, refer to lab 6 for instructions on how to get it installed.

If you still can't get Matplotlib to work, you can also disable visualization by commenting out the line

from display_svm import create_svm_graph</tt>

in train_svm.py and running train_svm with the argument show_graph=False. (If you do this, however, you may need to add print statements in order to answer some of the multiple-choice questions below: specifically, Questions 2 and 5-8. Also, you won't get to watch the SVM being trained!)

Your task: Update SVM from alpha values

Your task is to take the alpha values determined by SMO and use them to determine the support vectors, the normal vector w, and the offset b:

Any training point with alpha > 0 is a support vector.
w can be calculated using Equation 5.
If training is complete, b can be calculated using the gutter constraint (Equation 3). However, during training, the gutter constraint will produce different values of b depending on which support vector is used! To resolve this ambiguity, we will instead take the average of two values: the minimum value of b produced by a negative support vector, and the maximum value of b produced by a positive support vector. (Can you figure out why?)

Implement the function update_svm_from_alphas, which takes in a SupportVectorMachine, then uses the SVM's training points and alpha values to update w, b, and support_vectors. This function should return the updated SVM. (If the input SVM already has w, b, and/or support_vectors defined, ignore them and overwrite them. For this function, you may assume that the SVM is 2-dimensional and that it has at least one training point with alpha > 0.)

Important: Do NOT use svm.copy() in this function or instantiate a new SVM using the SupportVectorMachine constructor, as training (and the test cases) will likely fail.

def update_svm_from_alphas(svm):

train_svm will call update_svm_from_alphas, so once you've implemented it, you should be able to train an SVM on a dataset and visualize the results!

Arguments for `train_svm`

The function train_svm has only one required argument:

training_points: A list of training points as Point objects.

train_svm also has many optional arguments (with defaults given):

kernel_fn=dot_product: The kernel function (a function object) to be used in the SVM. Currently, the visualization only supports linear kernels (i.e. it can only draw straight lines).
max_iter=500: The maximum number of iterations to perform (an int). Each iteration consists of considering every pair of training points. (So if there are n training points, one iteration considers up to n² pairs of training points. Note that the visualization can update up to n times per iteration, not just once per iteration.)
show_graph=True: Boolean value indicating whether to display a graph of the SVM.
animate=True: Boolean value indicating whether to display updates on the SVM graph during training (only applies if show_graph is True).
animation_delay=0.5: Number of seconds to delay between graph updates (only applies if both show_graph and animate are True).
manual_animation=False: Boolean value indicating whether to pause execution after each animation update (only applies if show_graph is True). If True, you will need to manually close the graph window after each update. This option may be used as a work-around if normal animation isn't working on your machine.

We have also provided five sample datasets in svm_data.py:

sample_data_1 and sample_data_2, drawn with ASCII art near the top of train_svm.py
recit_data, the dataset from recitation and from Robert McIntyre's notes (although Robert labels the points A, B, C, D, whereas here they are called A, B, D, E)
harvard_mit_data, the Harvard/MIT data from 2014 Quiz 3, Problem 2, Part B
unseparable_data, the Harvard/MIT data with an additional MIT point at (4,4) that makes the data not linearly separable

How to run `train_svm`

Note that there is currently no command-line interface for train_svm, so if you use a command line, you can either change the parameters in train_svm.py and re-run it multiple times, or you can load it into an interactive Python shell by running the command python3 in a command line and then (in the Python shell) from train_svm import *.

If you just run train_svm.py, it will automatically run whatever functions are called at the bottom of the file (by default, training on sample_data_1). You can comment/uncomment the functions, change the arguments, and add additional functions.

In an interactive Python shell, you can call the function train_svm(my_data, ...) on the various datasets, using the arguments described above.

Part 6: Multiple Choice Questions about SVM Training

Questions 1-4: Running `train_svm`

For Questions 1-4, fill in the appropriate ANSWER_n with an integer.

Note: Adjusting the animation delay or other arguments above may be useful for answering some of these questions.

Question 1: Try training an SVM on the Harvard/MIT data from 2014 Quiz 3 (harvard_mit_data). How many iterations does it take?

Question 2: During training for the Harvard/MIT data, what is the maximum number of support vectors shown on the graph at once? (Assume that all training points with alpha > 0, displayed as circled points, are support vectors.)

Note: If you are using show_graph=False, one way to keep track of the number of support vectors is to record svm.support_vectors at every (graphical) iteration of training. See line 144 of train_svm.py for an example of where you can record the current set of support vectors in each iteration.

Question 3: After training for the Harvard/MIT data, how many support vectors are there?

Question 4: Try training an SVM on the recitation dataset (recit_data). How many iterations does it take?

Questions 5-10: Identifying points

For Questions 5-10, consider what happens as the SVM trains on the recitation data, which consists of four points: A(1,3), B(1,1), D(2,2), and E(3,2). (Note that this is different from the labeling in Robert McIntyre's notes -- he uses the same four points, but labeled A, B, C, D.)

If you are using show_graph=False, you may want to put a print statement near the SVM graph update line in train_svm. See line 144 of train_svm.py for an example of where you can put such a print statement.

For each question, fill in the appropriate ANSWER_n with a list of point names, selected from A, B, D, E (e.g. ['A', 'B', 'E']).

Question 5: When a boundary first appears on the graph, which points are support vectors?

Question 6: When a boundary first appears on the graph, which training points appear to lie on the gutters?

Question 7: When a boundary changes on the graph (i.e. the second boundary that appears), which points are support vectors?

Question 8: When a boundary changes on the graph (i.e. the second boundary that appears), which points appear to lie on the gutters?

Question 9: When training is complete, which points are support vectors?

Question 10: When training is complete, which points appear to lie on the gutters?

Questions 11-16: True/False

Answer the following questions about SVMs in general, assuming that the data is linearly separable. (You may want to consider the provided datasets as examples.)

For each question, fill in the appropriate ANSWER_n with True or False.

Question 11: During training, all support vectors lie on the gutters.

Question 12: After training, all support vectors lie on the gutters.

Question 13: During training, all points on the gutters are support vectors.

Question 14: After training, all points on the gutters are support vectors.

Question 15: During training, no points can lie between the gutters (i.e. in the margin).

Question 16: After training, no points can lie between the gutters (i.e. in the margin).

Questions 17-19: General Multiple Choice

Answer the following questions about SVMs in general, assuming that the data is linearly separable. (You may want to copy and modify one of the provided datasets to experimentally determine the answers.)

For each question, fill in the appropriate ANSWER_n with a list of all answers that apply (e.g. [1, 3]), from the following choices:

The decision boundary may change.
The decision boundary may stay the same.
The margin width may decrease.
The margin width may increase.
The margin width may stay the same.
The number of support vectors may decrease.
The number of support vectors may increase.
The number of support vectors may stay the same.

Question 17: If you start with a trained SVM and move one of the support vectors directly toward the decision boundary (i.e. in a direction perpendicular to the decision boundary and moving closer to the boundary), then retrain, what could happen?

Question 18: If you start with a trained SVM and move one of the support vectors directly away from the decision boundary (i.e. in a direction perpendicular to the decision boundary and moving away from the boundary), then retrain, what could happen?

Question 19: If you start with a trained SVM and move one of the support vectors along its gutter (parallel to the decision boundary), then retrain, what could happen?

Question 20: And if the data is NOT linearly separable...

Question 20: What does our SVM trainer do if the data is not linearly separable? (If you're not sure, try training on unseparable_data.)

Fill in ANSWER_20 with the one best answer as an int (e.g. 3):

It identifies outlier points and systematically eliminates them from the data to avoid overfitting.
It gradually relaxes constraints until a solution is found.
It determines that the data is not separable and raises an exception or returns None.
It determines that the data is not separable, so it instead returns the best available solution.
It continues attempting to find a solution until training terminates because the alpha values are no longer changing, due to convergence.
It continues attempting to find a solution until it times out by reaching the maximum number of iterations.

If you want to do more...

If you want to learn more about training SVMs, the following resources (mostly beyond the scope of 6.034) may be helpful:

SVM lecture notes from a machine-learning class at NYU
Paper on Sequential Minimal Optimization
SVM notes, from the Reference material and playlist
SVM slides, from the Reference material and playlist
Wikipedia articles on SVM math and Sequential Minimal Optimization

Possible extensions of this lab include:

Training on other datasets, such as ones from past quiz problems or from the internet
Defining some non-linear kernel functions and extend train_svm to handle them (primarily by adding a kernel_fn argument to your update_svm_from_alphas), then training with the alternate kernels
Extending the visualization code to display non-linear kernels
Extending train_svm to handle 1-D, 3-D, or higher-dimensional SVMs

If you do something cool, we'd love to see it! Feel free to send your code and/or results to 6.034-2018-staff@mit.edu (ideally with some sort of documentation). Your code could even end up in a future version of this lab! (With your permission, of course.)

API

The file svm_api.py defines the Point and SupportVectorMachine classes, as well as some helper functions for vector math, all described below.

`Point`

A Point object has the following attributes:

name: The name of the point (a string).

coords: The coordinates of the point, represented as a vector (a tuple or list of numbers).

classification: The true classification of the point, if known, as a number, typically +1 or -1. Initialized by default to None.

alpha: The supportiveness (alpha) value of the point, if assigned.

The Point class supports iteration, to iterate through the coordinates.

`SupportVectorMachine`

A SupportVectorMachine is a classifier that uses a decision boundary to classify points. The decision boundary is defined by a normal vector w (a vector, represented as a list or tuple of coordinates), and an offset b (a number). The SVM also has a list of training points and optionally a list of support vectors. You can access its parameters using these attributes:

w: The normal vector w.

b: The offset b.

training_points: A list of Point objects with known classifications.

support_vectors: A list of Point objects that serve as support vectors for the SVM. Every support vector is also a training point.

To set an SVM's decision boundary, you can modify the parameters w and b directly, or use...

set_boundary(new_w, new_b): Updates w and b, returning the modified SVM.

To instantiate a new SVM, use the constructor:

my_svm = SupportVectorMachine(w, b, training_points, support_vectors)

The SupportVectorMachine class also has a .copy() method for making a deep copy of an SVM.

Helper functions for vector math

vector_add(vec1, vec2): Given two vectors represented as iterable vectors (lists or tuples of coordinates) or Points, returns their vector sum as a list of coordinates.

scalar_mult(c, vec): Given a constant scalar and an iterable vector (as a tuple or list of coordinates) or a Point, returns a scaled list of coordinates.

Survey

Please answer these questions at the bottom of your lab file:

NAME: What is your name? (string)

COLLABORATORS: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)

HOW_MANY_HOURS_THIS_LAB_TOOK: Approximately how many hours did you spend on this lab? (number or string)

WHAT_I_FOUND_INTERESTING: Which parts of this lab, if any, did you find interesting? (string)

WHAT_I_FOUND_BORING: Which parts of this lab, if any, did you find boring or tedious? (string)

(optional) SUGGESTIONS: What specific changes would you recommend, if any, to improve this lab for future years? (string)

(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)

When you're done, run the online tester to submit your code.

Lab 8: Support Vector Machines

From 6.034 Wiki

Current revision

Contents

The More, the Merrier

The Support Vector Machine

Equation Reference

Part 1: Vector Math

Part 2: Using the SVM Boundary Equations

Part 3: Supportiveness

Supportiveness is never negative, and is 0 for non-support-vectors

Supportiveness values must be internally consistent

Part 4: Evaluating Accuracy

Part 5: Training a support vector machine

What `train_svm` does

Your task: Update SVM from alpha values

Arguments for `train_svm`

How to run `train_svm`

Part 6: Multiple Choice Questions about SVM Training

Questions 1-4: Running `train_svm`

Questions 5-10: Identifying points

Questions 11-16: True/False

Questions 17-19: General Multiple Choice

Question 20: And if the data is NOT linearly separable...

If you want to do more...

API

`Point`

`SupportVectorMachine`

Helper functions for vector math

Survey

Views

Personal tools

Navigation

Search

Toolbox

@@ Line 1: / Line 1: @@
+<!-- {{Unreleased}} -->
 __TOC__
-This lab is due by [todo] at 10:00pm.
+{{Lab_Due|when=Thursday, November 12}}
-To work on this lab, you will need to get the code:
+{{Get_Code|lab=8}}
-[todo]
-<!--The online tester is now available! Online tests will be made available by the end of Tuesday, November 10.  In the meantime, the local tester provides thorough unit tests for each section of the lab.-->
+== The More, the Merrier ==
-Your answers for this lab belong in the main file <tt>lab7.py</tt>.
+So far in 6.034, we've discussed a few different supervised machine learning algorithms:
+* '''k-nearest neighbors (kNN)''', which classify points based on which training points are nearby
+* '''identification trees (ID trees)''', which classify points using a tree-based exploration
+* '''neural networks (NN)''', which classify points by iteratively applying small, primitive mathematical operations on features
-= Problems =
+The Support Vector Machine (SVM) is yet another supervised machine learning algorithm. An SVM classifies a point by, conceptually, comparing it against the most "important" training points, which are called the ''support vectors''. The support vectors of classification ''C'' which are most similar to '''x''' win the vote, and '''x''' is consequently classified as ''C''. In this way, an SVM can be likened to doing nearest neighbors comparison.
-This lab is divided into two independent parts. In the first part, you'll code subroutines necessary for training and using neural networks. In the second part, you'll code subroutines for using and validating support vector machines.
+Importantly, SVMs can be very robust, as the principle paradigm of the SVM algorithm is that ''the classifier always maximizes the margin between the differently-classified data points''. Visually, if you imagine drawing a decision boundary in a plane to separate two different classifications of data, an SVM will always position the decision boundary in such a way as to maximize the distance to the closest training points.
-== Neural Nets ==
+You might find the following diagram (inspired by Robert McIntyre's notes) helpful as a visual reference throughout this lab:
+[[Image:SvmDiagram.jpg]]
-=== Wiring a neural net ===
+== The Support Vector Machine ==
-A neural net is composed of individual neurons, which generally take this form:
+An SVM is a numeric classifier. That means that all of the features of the data must be ''numeric'', not symbolic. Furthermore, in this class, we'll assume that the SVM is a ''binary'' classifier: that is, it classifies points as one of two classifications. We'll typically call the classifications "+" and "-".
+A trained SVM is defined by two values:
+* A normal vector '''w''' (also called the weight vector), which solely determines the shape and direction of the decision boundary.
+* A scalar offset '''b''', which solely determines the position of the decision boundary with respect to the origin.
-[[Image:Lab6_SimpleNeuron.png]]
+A trained SVM can then classify a point '''x''' by computing ''w · x + b''. If this value is positive, '''x''' is classified as +; otherwise, '''x''' is classified as -.
+The decision boundary is coerced by support vectors, so called because these vectors (data points) ''support'' the boundary: if any of these points are moved or eliminated, the decision boundary changes! All support vectors lie on a ''gutter'', which can be thought of as a line running parallel to the decision boundary. There are two gutters: one gutter hosts positive support vectors, and the other, negative support vectors.
+Note that, though a support vector is always on a gutter, it's '''not''' necessarily true that every data point on a gutter is a support vector.
-We form the net by combining the neurons into a structure, such as the example shown below.
+== Equation Reference ==
+Below are the five principle SVM equations, as taught in lecture and recitation. Equations 1-3 define the decision boundary and the margin width, while Equations 4 and 5 can be used to calculate the alpha (supportiveness) values for the training points.
-[[Image:Lab6_SimpleNeuralNet.png‎]]
+[[Image:Lab6 Eqns.png]]
+For more information about how to apply these equations, see:
+* [http://web.mit.edu/dxh/www/svm.html Dylan's guide to solving SVM quiz problems]
+* [http://web.mit.edu/dxh/www/rlm-svm-notes.pdf Robert McIntyre's SVM notes]
+* [https://ai6034.mit.edu/wiki/images/SVM_and_Boosting.pdf SVM notes], from the [[Reference material and playlist]]
-In a neural net with two inputs ''x'' and ''y'', each input-layer neuron draws a line and shades one side of it, satisfying the equation <tt>''ax + by >= T''</tt>.  The remaining neurons in the later layers of the neural net perform logic functions on the shadings.
+== Part 1: Vector Math ==
-Each of the following pictures can be produced by a neural net with two inputs ''x'' and ''y''.  For each one, determine the minimum number of neurons necessary to produce the picture.  Express your answer as a list indicating the number of nodes per layer.
+We'll start with some basic functions for manipulating vectors. For now, we will represent an ''n''-dimensional vector as a list or tuple of ''n'' coordinates. <tt>dot_product</tt> should compute the dot product of two vectors, while <tt>norm</tt> computes the length of a vector. Implement both functions.
-As an example, the neural net shown above would be represented by the list [3, 2, 3, 1].
+(If these look familiar, it's probably because you saw them on Lab 5. Feel free to copy your implementations from your <tt>lab5.py</tt>.)
-[[Image:Neural_net_pictures_2015.jpg]]
+ def dot_product(u, v):
-The last picture (<tt>nn_grid</tt>) is optional.  To test it locally, change the boolean flag <tt>TEST_NN_GRID</tt> to <tt>True</tt>.
+ def norm(v):
-'''Note''': If you downloaded the lab files in the first two hours after it was released, there was a mistake in the answer for <tt>nn_grid</tt>, which has since been corrected.
+Later, when you need to actually manipulate vectors, note that we have also provided methods for adding two vectors (<tt>vector_add</tt>) and for multiplying a scalar by a vector (<tt>scalar_mult</tt>). (See the [[#Helper_functions_for_vector_math|API]], below.)
-=== Neural net equations (reference only) ===
+== Part 2: Using the SVM Boundary Equations ==
-For reference, here are the fundamental equations that define a neural net:
+Equations 1 and 3 above describe how certain data points must interact with the SVM decision boundary and gutters.
-[[Image:Lab6_NN_Eqns.png]]
+We will start by leveraging Equation 1 to classify a point with a given SVM (ignoring the point's actual classification, if any). Per Equation 1,
+* a point's classification is +1 when <tt>w·x + b > 0</tt>
+* a point's classification is -1 when <tt>w·x + b < 0</tt>
-=== Helper functions ===
+If <tt>w·x + b = 0</tt>, the point lies on the decision boundary, so its classification is ambiguous.
-First, you'll code helper functions for the neural nets. The <tt>stairstep</tt> and <tt>sigmoid</tt> functions are threshold functions; each neuron in a neural net uses a threshold function to determine whether its input stimulation is large enough for it to emit a non-zero output.  Fill in each of the functions below.
-<tt>stairstep</tt>: Computes the output of the stairstep function using the given threshold (T)
+First, implement <tt>positiveness(svm, point)</tt> which evaluates the expression <tt>w·x + b</tt> to calculate how positive a point is. The first argument, <tt>svm</tt>, is a [[#SupportVectorMachine | <tt>SupportVectorMachine</tt> object]], and <tt>point</tt> is a [[#Point | <tt>Point</tt> object]].
-  def stairstep(x, threshold=0):
+  def positiveness(svm, point):
-<tt>sigmoid</tt>: Computes the output of the sigmoid function using the given steepness (S) and midpoint (M)
- def sigmoid(x, steepness=1, midpoint=0):
+Next, classify a point as +1 or -1. If the point lies on the boundary, return 0.
-For your convenience, the constant ''e'' is defined in <tt>lab6.py</tt>.
+ def classify(svm, point):
-The accuracy function is used when training the neural net with back propagation. It measures the performance of the neural net as a function of its desired output and its actual output (given some set of inputs).  Note that the accuracy function is symmetric -- that is, it doesn't care which argument is the desired output and which is the actual output.
+Next, use the SVM's current decision boundary to calculate its margin width (Equation 2):
-<tt>accuracy</tt>: Computes accuracy using <tt>desired_output</tt> and <tt>actual_output</tt>. If the neurons in the network are using the <tt>stairstep</tt> threshold function, the accuracy will range from -0.5 to 0
+ def margin_width(svm):
- def accuracy(desired_output, actual_output):
-=== Forward propagation ===
+Finally, we will check that the gutter constraint is satisfied with the SVM's current support vectors and boundary. The gutter constraint imposes two restrictions simultaneously:
+# The positiveness of a positive support vector must be +1, and the positiveness of a negative support vector must be -1.
+# No training point may lie strictly between the gutters. That is, each training point should have a positiveness value indicating that it either lies on a gutter or outside the margin.
-Next, you'll code forward propagation, which takes in a dictionary of inputs and computes the output of every neuron in a neural net. As part of coding forward propagation, you should understand how a single neuron computes its output as a function of its input: each input into the neuron is multiplied by the weight on the wire, the weighted inputs are summed together, and the sum is passed through a specified threshold function to produce the output.
+Note that the gutter constraint does not check whether points are classified ''correctly'': it just checks that the gutter constraint holds for the current assigned classification of a point.
-To compute the output of each neuron in a neural net, iterate over each neuron in the network in order, starting from the input neurons and working toward the output neuron. (Hint: The function <b><tt>net</tt></b><tt>.topological_sort()</tt> may be useful; see the [[#NeuralNet|API]] for details). The algorithm is called forward propagation because the outputs you calculate for earlier neurons will be propagated forward through the network and used to calculate outputs for later neurons.
+Implement <tt>check_gutter_constraint</tt>, which should return a set (not a list) of the training points that violate one or both conditions:
+ def check_gutter_constraint(svm):
-Implement the method <tt>forward_prop</tt>:
+== Part 3: Supportiveness ==
- def forward_prop(net, input_values, threshold_fn=stairstep):
-Here, <tt>net</tt> is a neural network, <tt>input_values</tt> is a dictionary mapping input variables to their values, and <tt>threshold_fn</tt> is a function that each neuron will use to decide what value to output. This function should return a tuple containing
-# The overall output value of the network, i.e. the output value associated with the output neuron of the network.
-# A dictionary mapping neurons to their immediate outputs.
-The dictionary of outputs is permitted to contain extra keys (for example, the input values). The function should <em>not</em> modify the neural net in any way.
+To train a support vector machine, every training point is assigned a supportiveness value (also known as an alpha value, or a Lagrange multiplier), representing how important the point is in determining (or "supporting") the decision boundary. The supportiveness values must satisfy a number of conditions, which we will explore below.
-=== Backward propagation ===
+=== Supportiveness is never negative, and is 0 for non-support-vectors ===
-Backward propagation is the process of training a neural network using a particular training point to modify the weights of the network, with the goal of improving the network's performance.
+First, implement <tt>check_alpha_signs</tt> to ensure that each point's supportiveness value satisfies two conditions:
+# Each training point should have a non-negative supportiveness.
+# Each support vector should have positive supportiveness, while each non-support vector should have a supportiveness of 0.
-To perform back propagation on a given training point, or set of inputs:
+Note: each point's supportiveness value can be accessed a property of the point. See the [[#Helper_functions_for_vector_math|API]] for more information.
-# Use forward propagation (with the sigmoid threshold function) to compute the output of each neuron in the network.
-# Compute the update coefficient <tt>delta_B</tt> for each neuron in the network, starting from the output neuron and working backward toward the input neurons. (The function <b><tt>net</tt></b><tt>.topological_sort()</tt> can be useful here; see the [[#NeuralNet|API]] for details).
-# Use the update coefficients <tt>delta_B</tt> to compute new weights for the network.
-# Update all of the weights in the network.
-You have already coded the <tt>forward_propagation</tt> routine. To complete the definition of back propagation, you'll define a helper function <tt>calculate_deltas</tt> for computing the update coefficients <tt>delta_B</tt> of each neuron in the network, and a function <tt>update_weights</tt> that retrieves the list of update coefficients using <tt>calculate_deltas</tt>, then modifies the weights of the network accordingly.
+This function, like <tt>check_gutter_constraint</tt> above, should return a set of the training points that violate either of the supportiveness conditions.
-Implement <tt>calculate_deltas</tt> to return a dictionary mapping neurons to update coefficients (<tt>delta_B</tt> values):
+ def check_alpha_signs(svm):
- def calculate_deltas(net, input_values, desired_output):
+=== Supportiveness values must be internally consistent ===
+Implement <tt>check_alpha_equations</tt> to check that the SVM's supportiveness values are:
+# consistent with its boundary equation, according to Equation 4, and
+# consistent with the classifications of its training points, according to Equation 5.
-Next, use <tt>calculate_deltas</tt> to implement <tt>update_weights</tt>, which performs a single step of back propagation.  The function should compute <tt>delta_B</tt> values and weight updates for entire neural net, then update all weights.  The function <tt>update_weights</tt> should return the modified neural net with appropriately updated weights.  (Hint: You can update the weight of a <tt>Wire</tt> instance by setting its <tt>wire.weight</tt> to a new value.)
+This function should return <tt>True</tt> if both Equations 4 and 5 are satisfied, otherwise <tt>False</tt>. Remember the <tt>vector_add</tt> and <tt>scalar_mult</tt> helper functions are given to you in the [[#Helper_functions_for_vector_math|API]] if you'd like to use them in your implementation.
-  def update_weights(net, input_values, desired_output, r=1):
+  def check_alpha_equations(svm):
+== Part 4: Evaluating Accuracy ==
-Now you're ready to complete the <tt>back_prop</tt> function, which continues to update weights in the neural net until the accuracy surpasses the accuracy threshold.  <tt>back_prop</tt> should return a tuple containing:
+Once a support vector machine has been trained -- or even while it is being trained -- we want to know how well it has classified the training data. Write a function that checks whether the training points were classified correctly and returns a set containing the training points that were misclassified, if any. Hint: You might find it helpful to use a function that you perviously defined.
-# The modified neural net, with trained weights
-# The number of iterations (that is, the number of weight updates)
-  def back_prop(net, input_values, desired_output, r=1, accuracy_threshold=-.001):
+  def misclassified_training_points(svm):
+== Part 5: Training a support vector machine ==
+So far, we have seen how to calculate the final parameters of an SVM (given the decision boundary), and we've used the equations to assess how well an SVM has been trained, but we haven't actually attempted to train an SVM.
-If your code is failing the <tt>back_prop</tt> tests but passing everything else:
+In practice, training an SVM is a hill-climbing problem in alpha-space using the Lagrangian.  There's a bit of math involved, and the equations are typically solved using Sequential Minimal Optimization (SMO), a type of quadratic programming (which is similar to linear programming, but more complicated).
-* Make sure you have the current version of tests.py and neural_net_api.py, which were updated on 11/7.
-* Make sure you're using <tt>out_A</tt> in the weight update formula (<tt>r * out_A * delta_B</tt>), not <tt>out_B</tt>.
-=== Extra Credit Project: Train a neural net on a dataset ===
+...but if that sounds scary, don't worry -- we've provided code to do most of it for you!
-In practice, we would want to use multiple training points to train a neural net, not just one.  There are many possible implementations -- for instance, you could put all the training points into a queue and perform back propagation with each point in turn.  Alternatively, you could use a multidimensional accuracy function and try to train with multiple training points simultaneously.
-Here are some examples of datasets that you could use to train a 2-input neural net:
+=== What <tt>train_svm</tt> does ===
+In train_svm.py, we've provided some SVM-solving code, originally written by past 6.034 student Crystal Pan.  Here is a very high-level pseudocode overview of what the function <tt>train_svm</tt> (in train_svm.py) does:
-. The letter L
 <pre>
-+ -
+while (alphas are still changing) and (iteration < max_iter):
-+ -
+    for i in training_points:
-+ -
+        for j in training_points:
-+ - - - -
+            Update i.alpha and j.alpha using SMO to minimize ||w|| (i.e. maximize the margin width)
-- + + + +
-1 2 3 4
-</pre>
-. This moat-like shape:
-<pre>
-- - - - -
--       -
--   +   -
--       -
-- - - - -
-1 2 3 4
-</pre>
-. This patchy shape:
-<pre>
-- -   + +
-- -   + +
-+ +   - -
-+ +   - -
-1 2 3 4
-</pre>
-It should be possible to train a 6-neuron neural net to classify any one of the three shapes.
+        Update the SVM's w, b, and support_vectors (using a function you'll write)
+        Update the displayed graph using display_svm.py
-For some unspecified amount of extra credit, extend your code and/or the API to train a neural net on multiple inputs.  The steps include:
+Print the final decision boundary and number of misclassified points
-* Wire up a neural net (see <tt>nn_problems.py</tt> for some examples)
+Return the trained SVM
-* Encode the training data (you can use one of the example datasets above, a quiz problem, or make up your own)
+</pre>
-* Develop an algorithm (e.g. extend your <tt>back_prop</tt> function) for training your neural net on multiple training points
-* Initialize your neural net with random weights
-* Train the neural net and see if it works!
-To receive your extra credit, send your code to 6.034-2015-support@mit.edu '''by December 4, 2015''', ideally with some sort of documentation.  (Briefly explain what you did and how you did it.)
+We've also provided visualization code in <tt>display_svm.py</tt>, originally written by past 6.034 student Kelly Shen. This code is automatically called by <tt>train_svm</tt>, although you can adjust the parameters (or disable graphing) by calling <tt>train_svm</tt> with [[#Arguments for train_svm|additional arguments]].
-== Support Vector Machines ==
+Note that the visualization requires the Python module Matplotlib. If you don't currently have Matplotlib, [https://ai6034.mit.edu/wiki/index.php?title=Lab_6#What_if_I_don.27t_have_Matplotlib_and_NumPy.3F refer to lab 6 for instructions on how to get it installed].
-=== Vector Math ===
+If you still can't get Matplotlib to work, you can also disable visualization by commenting out the line
-We'll start with some basic functions for manipulating vectors.  For now, we will represent an ''n''-dimensional vector as a list or tuple of ''n'' coordinates.
+  from display_svm import create_svm_graph</tt>
-<tt>dot_product</tt> should compute the dot product of two vectors, while <tt>norm</tt> computes the length of a vector.  (There is a simple implementation of <tt>norm</tt> that uses <tt>dot_product</tt>.)  Implement both functions:
+in <tt>train_svm.py</tt> and running <tt>train_svm</tt> with the argument <tt>show_graph=False</tt>. (If you do this, however, you may need to add print statements in order to answer some of the multiple-choice questions below: specifically, Questions 2 and 5-8. Also, you won't get to watch the SVM being trained!)
- def dot_product(u, v):
+=== Your task: Update SVM from alpha values ===
- def norm(v):
+Your task is to take the alpha values determined by SMO and use them to determine the support vectors, the normal vector '''w''', and the offset '''b''':
+* Any training point with alpha > 0 is a support vector.
+* <tt>w</tt> can be calculated using Equation 5.
+* If training is complete, <tt>b</tt> can be calculated using the gutter constraint (Equation 3). However, during training, the gutter constraint will produce different values of <tt>b</tt> depending on which support vector is used! To resolve this ambiguity, we will instead take the average of two values: the ''minimum'' value of <tt>b</tt> produced by a ''negative'' support vector, and the ''maximum'' value of <tt>b</tt> produced by a ''positive'' support vector. (Can you figure out why?)
+Implement the function <tt>update_svm_from_alphas</tt>, which takes in a <tt>SupportVectorMachine</tt>, then uses the SVM's training points and alpha values to update <tt>w</tt>, <tt>b</tt>, and <tt>support_vectors</tt>. This function should return the updated SVM. (If the input SVM already has <tt>w</tt>, <tt>b</tt>, and/or <tt>support_vectors</tt> defined, ignore them and overwrite them.  For this function, you may assume that the SVM is 2-dimensional and that it has at least one training point with alpha > 0.)
-Later, when you need to actually manipulate vectors, note that we have also provided methods for adding two vectors (<tt>vector_add</tt>) and for multiplying a scalar by a vector (<tt>scalar_mult</tt>).  (See the [[#Helper_functions_for_vector_math|API]], below.)
+'''Important''': Do NOT use <tt>svm.copy()</tt> in this function or instantiate a new SVM using the <tt>SupportVectorMachine</tt> constructor, as training (and the test cases) will likely fail.
-=== SVM Equations (reference only) ===
+  def update_svm_from_alphas(svm):
-Next, we will use the following five SVM equations.  Recall from recitation that Equations 1-3 define the decision boundary and the margin width, while Equations 4 & 5 can be used to calculate the alpha (supportiveness) values for the training points.
-[[Image:Lab6 Eqns.png]]
+<tt>train_svm</tt> will call <tt>update_svm_from_alphas</tt>, so once you've implemented it, you should be able to train an SVM on a dataset and visualize the results!
+=== Arguments for <tt>train_svm</tt> ===
-For more information about how to apply these equations, see:
+The function <tt>train_svm</tt> has only one '''required''' argument:
-* [http://web.mit.edu/dxh/www/svm.html Dylan's guide to solving SVM quiz problems]
+* <tt><b>training_points</b></tt>: A list of training points as <tt>Point</tt> objects.
-* [http://web.mit.edu/dxh/www/rlm-svm-notes.pdf Robert McIntyre's SVM notes]
-* [https://ai6034.mit.edu/wiki/images/SVM_and_Boosting.pdf SVM notes], from the [[Reference material and playlist]]
-=== Using the SVM Boundary Equations ===
+<tt>train_svm</tt> also has many optional arguments (with defaults given):
+* <tt><b>kernel_fn</b>=dot_product</tt>: The kernel function (a <tt>function</tt> object) to be used in the SVM.  Currently, the visualization only supports linear kernels (i.e. it can only draw straight lines).
+* <tt><b>max_iter</b>=500</tt>: The maximum number of iterations to perform (an <tt>int</tt>).  Each iteration consists of considering every pair of training points.  (So if there are ''n'' training points, one iteration considers up to ''n''<sup>2</sup> pairs of training points.  Note that the visualization can update up to ''n'' times ''per'' iteration, not just once per iteration.)
+* <tt><b>show_graph</b>=True</tt>: Boolean value indicating whether to display a graph of the SVM.
+* <tt><b>animate</b>=True</tt>: Boolean value indicating whether to display updates on the SVM graph during training (only applies if <tt>show_graph</tt> is <tt>True</tt>).
+* <tt><b>animation_delay</b>=0.5</tt>: Number of seconds to delay between graph updates (only applies if both <tt>show_graph</tt> and <tt>animate</tt> are <tt>True</tt>).
+* <tt><b>manual_animation</b>=False</tt>: Boolean value indicating whether to pause execution after each animation update (only applies if <tt>show_graph</tt> is <tt>True</tt>).  If <tt>True</tt>, you will need to manually close the graph window after each update. This option may be used as a work-around if normal animation isn't working on your machine.
-We will start by using Equation 1 to classify a point with a given SVM, ignoring the point's actual classification (if any).  According to Equation 1, a point's classification is +1 when <tt>w·x + b > 0</tt>, or -1 when <tt>w·x + b < 0</tt>.  If <tt>w·x + b = 0</tt>, the point lies on the decision boundary, so its classification is ambiguous.
+We have also provided five sample datasets in <tt>svm_data.py</tt>:
+* <tt>sample_data_1</tt> and <tt>sample_data_2</tt>, drawn with ASCII art near the top of <tt>train_svm.py</tt>
+* <tt>recit_data</tt>, the dataset from recitation and from [http://web.mit.edu/dxh/www/rlm-svm-notes.pdf Robert McIntyre's notes] (although Robert labels the points A, B, C, D, whereas here they are called A, B, D, E)
+* <tt>harvard_mit_data</tt>, the Harvard/MIT data from [http://courses.csail.mit.edu/6.034f/Examinations/2014q3.pdf 2014 Quiz 3, Problem 2, Part B]
+* <tt>unseparable_data</tt>, the Harvard/MIT data with an additional MIT point at (4,4) that makes the data not linearly separable
-First, evaluate the expression <tt>w·x + b</tt> to calculate how positive a point is.  <tt>svm</tt> is a <tt>SupportVectorMachine</tt> object, and <tt>point</tt> is a <tt>Point</tt> (see the [[#Support_Vector_Machines_2|API]] below for details).
+=== How to run <tt>train_svm</tt> ===
- def positiveness(svm, point):
+Note that there is currently no command-line interface for <tt>train_svm</tt>, so if you use a command line, you can either change the parameters in <tt>train_svm.py</tt> and re-run it multiple times, or you can load it into an interactive Python shell by running the command <tt>python3</tt> in a command line and then (in the Python shell) <tt>from train_svm import *</tt>.
+If you just run <tt>train_svm.py</tt>, it will automatically run whatever functions are called at the bottom of the file (by default, training on <tt>sample_data_1</tt>). You can comment/uncomment the functions, change the arguments, and add additional functions.
-Next, classify a point as +1 or -1.  If the point lies on the boundary, return 0.
+In an interactive Python shell, you can call the function <tt>train_svm(my_data, ...)</tt> on the various datasets, using the [[#Arguments for train_svm|arguments described above]].
- def classify(svm, point):
+== Part 6: Multiple Choice Questions about SVM Training ==
+=== Questions 1-4: Running <tt>train_svm</tt> ===
-Then, use the SVM's current decision boundary to calculate its margin width (Equation 2):
+For Questions 1-4, fill in the appropriate <tt>ANSWER_n</tt> with an integer.
- def margin_width(svm):
+:Note: Adjusting the animation delay or other arguments above may be useful for answering some of these questions.
+;Question 1
+:Try training an SVM on the Harvard/MIT data from [http://courses.csail.mit.edu/6.034f/Examinations/2014q3.pdf 2014 Quiz 3] (<tt>harvard_mit_data</tt>). How many iterations does it take?
-Finally, we will check that the gutter constraint is satisfied.  The gutter constraint requires that positiveness be +1 for positive support vectors, and -1 for negative support vectors.  Our function will also check that no training points lie between the gutters -- that is, every training point should have a positiveness value indicating that it either lies on a gutter or outside the margin.  (Note that the gutter constraint does not check whether points are classified correctly.)  Implement <tt>check_gutter_constraint</tt>, which should return a set (not a list) of the training points that violate one or both conditions:
+;Question 2
+:During training for the Harvard/MIT data, what is the maximum number of support vectors shown on the graph at once? (Assume that all training points with alpha > 0, displayed as circled points, are support vectors.)
- def check_gutter_constraint(svm):
+:Note: If you are using <tt>show_graph=False</tt>, one way to keep track of the number of support vectors is to record <tt>svm.support_vectors</tt> at every (graphical) iteration of training. See line 144 of <tt>train_svm.py</tt> for an example of where you can record the current set of support vectors in each iteration.
-=== Using the Supportiveness Equations ===
+;Question 3
+:''After'' training for the Harvard/MIT data, how many support vectors are there?
-To train a support vector machine, every training point is assigned a supportiveness value (also known as an alpha value, or a Lagrange multiplier), representing how important the point is in determining (or "supporting") the decision boundary.  The supportiveness values must satisfy a number of conditions, which we will check below.
+;Question 4
+:Try training an SVM on the recitation dataset (<tt>recit_data</tt>). How many iterations does it take?
-First, implement <tt>check_alpha_signs</tt> to check each point's supportiveness value.  Each training point should have a non-negative supportiveness.  Specifically, all support vectors should have positive supportiveness, while all non-support vectors should have a supportiveness of 0.  This function, like <tt>check_gutter_constraint</tt> above, should return a set of the training points that violate either of the supportiveness conditions.
+=== Questions 5-10: Identifying points ===
- def check_alpha_signs(svm):
+For Questions 5-10, consider what happens as the SVM trains on the recitation data, which consists of four points: A(1,3), B(1,1), D(2,2), and E(3,2). (Note that this is different from the labeling in Robert McIntyre's notes -- he uses the same four points, but labeled A, B, C, D.)
+If you are using <tt>show_graph=False</tt>, you may want to put a print statement near the SVM graph update line in <tt>train_svm</tt>. See line 144 of <tt>train_svm.py</tt> for an example of where you can put such a print statement.
-Implement <tt>check_alpha_equations</tt> to check that the SVM's supportiveness values are consistent with its boundary equation and the classifications of its training points.  Return <tt>True</tt> if both Equations 4 and 5 are satisfied, otherwise False.
+For each question, fill in the appropriate <tt>ANSWER_n</tt> with a list of point names, selected from A, B, D, E (e.g. <tt>['A', 'B', 'E']</tt>).
- def check_alpha_equations(svm):
+;Question 5
+:When a boundary '''first appears''' on the graph, which points '''are support vectors'''?
-=== Classification Accuracy ===
+;Question 6
-Once a support vector machine has been trained -- or even while it is being trained -- we want to know how well it has classified the training data.  Write a function that checks whether the training points were classified correctly and returns a set containing the training points that were misclassified, if any.
+:When a boundary '''first appears''' on the graph, which training points '''appear to lie on the gutters'''?
- def misclassified_training_points(svm):
+;Question 7
+:When a boundary '''changes''' on the graph (i.e. the second boundary that appears), which points '''are support vectors'''?
+;Question 8
+:When a boundary '''changes''' on the graph (i.e. the second boundary that appears), which points '''appear to lie on the gutters'''?
-=== Extra Credit Project: Train a support vector machine ===
+;Question 9
-In class and in this lab, we have seen how to calculate the final parameters of an SVM (given the decision boundary), and we've used the equations to assess how well an SVM has been trained, but we haven't actually attempted to train an SVM.  In practice, training an SVM is a hill-climbing problem in alpha-space using the Lagrangian.  There's a bit of math involved.  The following resources may be helpful:
+:When '''training is complete''', which points '''are support vectors'''?
-* [http://cs.nyu.edu/~dsontag/courses/ml12/slides/lecture5.pdf SVM lecture notes] from a machine-learning class at NYU
-* [http://www-ai.cs.uni-dortmund.de/LEHRE/SEMINARE/SS09/AKTARBEITENDESDM/LITERATUR/PlattSMO.pdf paper on Sequential Minimal Optimization]
-* [https://ai6034.mit.edu/wiki/images/SVM_and_Boosting.pdf SVM notes], from the [[Reference material and playlist]]
-* [http://courses.csail.mit.edu/6.034f/ai3/SVM.pdf SVM slides], from the [[Reference material and playlist]]
-* Wikipedia articles on [https://en.wikipedia.org/wiki/Support_vector_machine#Linear_SVM SMV math] and [https://en.wikipedia.org/wiki/Sequential_minimal_optimization Sequential Minimal Optimization]
+;Question 10
+:When '''training is complete''', which points '''appear to lie on the gutters'''?
-For some unspecified amount of extra credit, extend your code and/or the API to train a support vector machine.  Possible extensions include implementing kernel functions or writing code to graphically display your training data and SVM boundary.  If you can come up with a reasonably simple procedure for training an SVM, preferably using only built-in Python packages, we may even use your code in a future 6.034 lab!  (With your permission, of course.)
+=== Questions 11-16: True/False ===
-To receive your extra credit, send your code to 6.034-2015-support@mit.edu '''by December 4, 2015''', ideally with some sort of documentation.  (Briefly explain what you did and how you did it.)
+Answer the following questions about SVMs ''in general'', assuming that the data is linearly separable. (You may want to consider the provided datasets as examples.)
-== Survey ==
+For each question, fill in the appropriate <tt>ANSWER_n</tt> with <tt>True</tt> or <tt>False</tt>.
-Please answer these questions at the bottom of your <tt>lab6.py</tt> file:
-* <tt>NAME</tt>: What is your name? (string)
+;Question 11
+:During training, all support vectors lie on the gutters.
-* <tt>COLLABORATORS</tt>: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)
+;Question 12
+:''After'' training, all support vectors lie on the gutters.
-* <tt>HOW_MANY_HOURS_THIS_LAB_TOOK</tt>: Approximately how many hours did you spend on this lab? (number or string)
+;Question 13
+:During training, all points on the gutters are support vectors.
-* <tt>WHAT_I_FOUND_INTERESTING</tt>: Which parts of this lab, if any, did you find interesting? (string)
+;Question 14
+:''After'' training, all points on the gutters are support vectors.
-* <tt>WHAT_I_FOUND_BORING</tt>: Which parts of this lab, if any, did you find boring or tedious? (string)
+;Question 15
+:During training, no points can lie between the gutters (i.e. in the margin).
-* (optional) <tt>SUGGESTIONS</tt>: What specific changes would you recommend, if any, to improve this lab for future years? (string)
+;Question 16
+:''After'' training, no points can lie between the gutters (i.e. in the margin).
+=== Questions 17-19: General Multiple Choice ===
-(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)
+Answer the following questions about SVMs ''in general'', assuming that the data is linearly separable. (You may want to copy and modify one of the provided datasets to experimentally determine the answers.)
-When you're done, run the online tester to submit your code.
+For each question, fill in the appropriate <tt>ANSWER_n</tt> with a list of all answers that apply (e.g. <tt>[1, 3]</tt>), from the following choices:
-= API =
+# The decision boundary may change.
+# The decision boundary may stay the same.
+# The margin width may decrease.
+# The margin width may increase.
+# The margin width may stay the same.
+# The number of support vectors may decrease.
+# The number of support vectors may increase.
+# The number of support vectors may stay the same.
-== Neural Nets ==
+;Question 17
-The file <tt>neural_net_api.py</tt> defines the <tt>Wire</tt> and <tt>NeuralNet</tt> classes, described below.
+:If you start with a trained SVM and move one of the support vectors ''directly toward'' the decision boundary (i.e. in a direction perpendicular to the decision boundary and moving closer to the boundary), then retrain, what could happen?
-=== NeuralNet ===
+;Question 18
-A neural net is represented as a directed graph whose edges are Wires and nodes can be neurons, inputs, or the output OUT.
+:If you start with a trained SVM and move one of the support vectors ''directly away from'' the decision boundary (i.e. in a direction perpendicular to the decision boundary and moving away from the boundary), then retrain, what could happen?
-A <tt>NeuralNet</tt> has the following attributes:
+;Question 19
-<ul>
+:If you start with a trained SVM and move one of the support vectors ''along its gutter'' (parallel to the decision boundary), then retrain, what could happen?
-<li><b><tt>net</tt></b><tt>.inputs</tt>, a list of named inputs to the network. An input can be either variable or constant: Variable inputs are represented by strings denoting their names, while constant inputs are represented as numbers (eg -1).</li>
-<li><b><tt>net</tt></b><tt>.neurons</tt>, a list of neurons. Neurons are represented as strings denoting their names.</li>
-<li><b><tt>net</tt></b><tt>.wires</tt>, a list of the wires (edges) that connect the nodes in the network. Each wire is a <tt>Wire</tt> object (see below.)</li>
-</ul>
-In this lab, inputs are supplied to neural nets in the form of a dictionary <tt>input_values</tt> that associates each named (variable) input with an input value.
+=== Question 20: And if the data is NOT linearly separable... ===
-The constant string <tt>NeuralNet.OUT</tt> represents the final output of a neural net.  It is not a neuron, but it is connected to the output neuron by a wire with weight 1.
+;Question 20
+:What does our SVM trainer do if the data is ''not'' linearly separable? (If you're not sure, try training on <tt>unseparable_data</tt>.)
+:Fill in <tt>ANSWER_20</tt> with the '''one''' best answer as an <tt>int</tt> (e.g. <tt>3</tt>):
+:# It identifies outlier points and systematically eliminates them from the data to avoid overfitting.
+:# It gradually relaxes constraints until a solution is found.
+:# It determines that the data is not separable and raises an exception or returns None.
+:# It determines that the data is not separable, so it instead returns the best available solution.
+:# It continues attempting to find a solution until training terminates because the alpha values are no longer changing, due to convergence.
+:# It continues attempting to find a solution until it times out by reaching the maximum number of iterations.
-You can retrieve the nodes (neurons, inputs, or <tt>NeuralNet.OUT</tt>) in a network:
+== If you want to do more... ==
-<ul>
-<li><b><tt>net</tt></b><tt>.get_incoming_neighbors(node)</tt>. Return a list of the nodes which are connected as inputs to <tt>node</tt></li>
-<li><b><tt>net</tt></b><tt>.get_outgoing_neighbors(node)</tt>. Return a list of the nodes to which <tt>node</tt> sends its output.</li>
-<li><b><tt>net</tt></b><tt>.get_output_neuron()</tt>. Return the output neuron of the network, which is the neuron that leads to <tt>NeuralNet.OUT</tt>. (In this lab, each neural net has exactly one output neuron.)</li>
-<li><b><tt>net</tt></b><tt>.topological_sort()</tt>. Return a sorted list of all the neurons in the network. The list is "topologically" sorted, which means that each neuron appears in the list after all the neurons that provide its inputs. Thus, the input layer neurons are first, the output neuron is last, etc.</li>
-</ul>
+If you want to learn more about training SVMs, the following resources (mostly beyond the scope of 6.034) may be helpful:
+* [http://cs.nyu.edu/~dsontag/courses/ml12/slides/lecture5.pdf SVM lecture notes] from a machine-learning class at NYU
+* [http://www-ai.cs.uni-dortmund.de/LEHRE/SEMINARE/SS09/AKTARBEITENDESDM/LITERATUR/PlattSMO.pdf Paper on Sequential Minimal Optimization]
+* [https://ai6034.mit.edu/wiki/images/SVM_and_Boosting.pdf SVM notes], from the [[Reference material and playlist]]
+* [http://courses.csail.mit.edu/6.034f/ai3/SVM.pdf SVM slides], from the [[Reference material and playlist]]
+* Wikipedia articles on [https://en.wikipedia.org/wiki/Support_vector_machine#Linear_SVM SVM math] and [https://en.wikipedia.org/wiki/Sequential_minimal_optimization Sequential Minimal Optimization]
-You can also retrieve the wires:
-<ul>
-<li><b><tt>net</tt></b><tt>.get_wires(startNode=None, endNode=None)</tt>. Return a list of all the wires in the network. If <tt>startNode</tt> or <tt>endNode</tt> are provided, returns only wires that start/end at particular nodes. Note that there is a wire leading from the output neuron to <tt>NeuralNet.OUT</tt> whose weight should always be 1.</li>
-<li><b><tt>net</tt></b><tt>.get_incoming_wires(node)</tt>. Return a list of wires that feed in to the given node.</li>
-<li><b><tt>net</tt></b><tt>.get_outgoing_wires(node)</tt>. Return a list of wires that the node feeds into.  (That is, wires that lead out of the node.)</li>
-</ul>
+Possible extensions of this lab include:
+* Training on other datasets, such as ones from past quiz problems or from the internet
+* Defining some non-linear kernel functions and extend train_svm to handle them (primarily by adding a <tt>kernel_fn</tt> argument to your <tt>update_svm_from_alphas</tt>), then training with the alternate kernels
+* Extending the visualization code to display non-linear kernels
+* Extending <tt>train_svm</tt> to handle 1-D, 3-D, or higher-dimensional SVMs
-Finally, you can query the parts of the network:
-<ul>
-<li><b><tt>net</tt></b><tt>.has_incoming_neuron(node)</tt>. Returns True if the node has at least one incoming neuron, otherwise False. (''Note: this method was added on 11/7'')</li>
-<!--<li><b><tt>net</tt></b><tt>.is_input_neuron(node)</tt>. Return True if the node is connected directly to an input, otherwise False.</li>-->
-<li><b><tt>net</tt></b><tt>.is_output_neuron(neuron)</tt>. Return True if the neuron is the final, output neuron in the network, otherwise False.</li>
-<li><b><tt>net</tt></b><tt>.is_connected(startNode, endNode)</tt>. Return True if there is a wire from startNode to endNode in the network, otherwise False.</li>
-</ul>
-<!--
+If you do something cool, we'd love to see it!  Feel free to send your code and/or results to 6.034-2018-staff@mit.edu (ideally with some sort of documentation). Your code could even end up in a future version of this lab! (With your permission, of course.)
-Note that:
-- Each variable input is represented by its name (a string).
+== API ==
-- Each constant input is represented by an int or float (eg -1).
+The file <tt>svm_api.py</tt> defines the <tt>Point</tt> and <tt>SupportVectorMachine</tt> classes, as well as some helper functions for vector math, all described below.
-- Each neuron is represented by its name (a string).
+=== <tt>Point</tt> ===
-- The final output is represented by the constant string <tt>NeuralNet.OUT</tt>.
+A <tt>Point</tt> object has the following attributes:
+;<tt>name</tt>
+:The name of the point (a string).
-The following methods are available for you to use:
+;<tt>coords</tt>
+:The coordinates of the point, represented as a vector (a tuple or list of numbers).
-<tt>get_wires(startNode=None, endNode=None)</tt>: Returns a list of all the wires in the graph.  If the start or end are provided, it restricts to wires that start/end at particular nodes. (A node can be an input, a neuron, or the output OUT.)
+;<tt>classification</tt>
+:The true classification of the point, if known, as a number, typically +1 or -1. Initialized by default to None.
-<tt>get_incoming_neighbors(node)</tt>: Returns an alphabetical list of neighboring nodes (neurons or inputs) that appear earlier in the neural net. That is, nodes that have wires leading into the provided node. Each node appears at most once.
+;<tt>alpha</tt>
+:The supportiveness (alpha) value of the point, if assigned.
-<tt>get_outgoing_neighbors(node)</tt>: Returns an alphabetical list of neighboring nodes (either be neurons or OUT) that appear later in the neural net (that is, nodes that receive the provided node's output). Each node appears at most once.
+The <tt>Point</tt> class supports iteration, to iterate through the coordinates.
-<tt>get_incoming_wires(endNode)</tt>: Returns a list of wires leading into the provided neuron or OUT.
+=== <tt>SupportVectorMachine</tt> ===
-<tt>get_outgoing_wires(startNode)</tt>: Returns a list of wires exiting out of the provided neuron or input.
+A <tt>SupportVectorMachine</tt> is a classifier that uses a decision boundary to classify points.  The decision boundary is defined by a normal vector <tt>w</tt> (a vector, represented as a list or tuple of coordinates), and an offset <tt>b</tt> (a number). The SVM also has a list of training points and optionally a list of support vectors.  You can access its parameters using these attributes:
-<tt>get_wire(startNode, endNode)</tt>: Returns the wire that directly connects startNode to endNode or None if no such wire exists.
+;<tt>w</tt>
+:The normal vector '''w'''.
-<tt>is_connected(startNode, endNode)</tt>: Returns True if there is a wire that connects startNode to endNode or False if no such wire exists.
+;<tt>b</tt>
+:The offset '''b'''.
-<tt>is_input_neuron(neuron)</tt>: Returns True if neuron is an input-layer neuron, else False.
+;<tt>training_points</tt>
+:A list of <tt>Point</tt> objects with known classifications.
-<tt>is_output_neuron(neuron)</tt>: Returns True if neuron is an output-layer neuron, else False.
+;<tt>support_vectors</tt>
--->
+:A list of <tt>Point</tt> objects that serve as support vectors for the SVM. Every support vector is also a training point.
-=== Wire ===
+To set an SVM's decision boundary, you can modify the parameters <tt>w</tt> and <tt>b</tt> directly, or use...
-A <tt>Wire</tt> is represented as a weighted, directed edge in a graph.  A wire can connect an input to a neuron, a neuron to a neuron, or a neuron to <tt>NeuralNet.OUT</tt>.  A wire's attributes are:
-<ul>
-<li><b><tt>wire</tt></b><tt>.startNode</tt>, the input or neuron at which the wire starts.  An input can be either a string or a number (eg -1).</li>
-<li><b><tt>wire</tt></b><tt>.endNode</tt>, the neuron (or <tt>NeuralNet.OUT</tt>) at which the wire ends.</li>
-<li><b><tt>wire</tt></b><tt>.weight</tt>, the weight on the wire (a float or int).</li>
-</ul>
-== Support Vector Machines ==
+;<tt>set_boundary(new_w, new_b)</tt>
-The file <tt>svm_api.py</tt> defines the <tt>Point</tt>, <tt>DecisionBoundary</tt>, and <tt>SupportVectorMachine</tt> classes, as well as some helper functions for vector math, all described below.
+:Updates <tt>w</tt> and <tt>b</tt>, returning the modified SVM.
-=== Point ===
+To instantiate a new SVM, use the constructor:
-A <tt>Point</tt> has the following attributes:
+:<tt>my_svm = SupportVectorMachine(w, b, training_points, support_vectors)</tt>
-<ul>
-<li><b><tt>point</tt></b><tt>.name</tt>, the name of the point (a string).</li>
-<li><b><tt>point</tt></b><tt>.coords</tt>, the coordinates of the point, represented as a vector (a tuple or list of numbers).</li>
-<li><b><tt>point</tt></b><tt>.classification</tt>, the classification of the point, if known.  Note that classification (if any) is a number, typically +1 or -1.</li>
-<li><b><tt>point</tt></b><tt>.alpha</tt>, the supportiveness (alpha) value of the point, if assigned.</li>
-</ul>
+The <tt>SupportVectorMachine</tt> class also has a <tt>.copy()</tt> method for making a deep copy of an SVM.
-=== DecisionBoundary ===
+=== Helper functions for vector math ===
-A <tt>DecisionBoundary</tt> is defined by two parameters: a normal vector <tt>w</tt>, and an offset <tt>b</tt>.  <tt>w</tt> is represented as a vector: a list or tuple of coordinates.  You can access these parameters using the attributes <tt>.w</tt> and <tt>.b</tt>.
+;<tt>vector_add(vec1, vec2)</tt>
+:Given two vectors represented as iterable vectors (lists or tuples of coordinates) or <tt>Points</tt>, returns their vector sum as a list of coordinates.
-=== SupportVectorMachine ===
+;<tt>scalar_mult(c, vec)</tt>
-A <tt>SupportVectorMachine</tt> is a classifier that uses a DecisionBoundary to classify points.  It has a list of training points and optionally a list of support vectors.  You can access these parameters using these attributes:
+:Given a constant scalar and an iterable vector (as a tuple or list of coordinates) or a <tt>Point</tt>, returns a scaled list of coordinates.
-<ul>
-<li><b><tt>svm</tt></b><tt>.boundary</tt>, the SVM's <tt>DecisionBoundary</tt>.</li>
-<li><b><tt>svm</tt></b><tt>.training_points</tt>, a list of <tt>Point</tt> objects with known classifications.</li>
-<li><b><tt>svm</tt></b><tt>.support_vectors</tt>, a list of <tt>Point</tt> objects that serve as support vectors for the SVM.  Every support vector is also a training point.</li>
-</ul>
-=== Helper functions for vector math ===
-<tt>vector_add</tt>: Given two vectors represented as lists or tuples of coordinates, returns their sum as a list of coordinates.
-<tt>scalar_mult</tt>: Given a constant scalar and a vector (as a tuple or list of coordinates), returns a scaled list of coordinates.
+{{Survey}}

Lab 8: Support Vector Machines

From 6.034 Wiki

Current revision

Contents

The More, the Merrier

The Support Vector Machine

Equation Reference

Part 1: Vector Math

Part 2: Using the SVM Boundary Equations

Part 3: Supportiveness

Supportiveness is never negative, and is 0 for non-support-vectors

Supportiveness values must be internally consistent

Part 4: Evaluating Accuracy

Part 5: Training a support vector machine

What train_svm does

Your task: Update SVM from alpha values

Arguments for train_svm

How to run train_svm

Part 6: Multiple Choice Questions about SVM Training

Questions 1-4: Running train_svm

Questions 5-10: Identifying points

Questions 11-16: True/False

Questions 17-19: General Multiple Choice

Question 20: And if the data is NOT linearly separable...

If you want to do more...

API

Point

SupportVectorMachine

Helper functions for vector math

Survey

Views

Personal tools

Navigation

Search

Toolbox

What `train_svm` does

Arguments for `train_svm`

How to run `train_svm`

Questions 1-4: Running `train_svm`

`Point`

`SupportVectorMachine`