Lab 5: Bayes Nets
From 6.034 Wiki
Contents |
This lab is due by Thursday, October 22 at 10:00pm.
Before working on the lab, you will need to get the code. You can...
- Use Git on your computer: git clone username@athena.dialup.mit.edu:/mit/6.034/www/labs/fall2020/lab5
- Use Git on Athena: git clone /mit/6.034/www/labs/fall2020/lab5
- Download it as a ZIP file: http://web.mit.edu/6.034/www/labs/fall2020/lab5/lab5.zip
- View the files individually: http://web.mit.edu/6.034/www/labs/fall2020/lab5/
All of your answers belong in the main file lab5.py. To submit your lab to the test server, you will need to download your key.py file and put it in either your lab5 directory or its parent directory. You can also view all of your lab submissions and grades here.
The world is an uncertain place
So far in 6.034, we have discussed various machine learning methods that are used to classify data in different ways. Such methods have included k-nearest neighbors, support vector machines, and neural networks. These machine learning algorithms train on and predict classifications for data points that have definitive features, such as "height", "likes-garlic", or more mathematically abstract features like numbers x and y.
Unfortunately, the world is not so cut-and-dried. Often, we deal with features that may exist, values that fall somewhere within a distribution, or events that happen with some likelihood. As such, in this lab, we will be exploring the world of probability as well as Bayesian networks which encode certain assumptions in probability.
Bayesian Networks encode independence assumptions
As described in lecture and recitation, events might be marginally or conditionally independent.
- A and B are said to be marginally independent when
- A is said to be conditionally independent of B given C when
A Bayesian Network (also known as a Bayes Net) is a graphical model that encodes assumptions of conditional independence between certain events (variables). This assumption of conditional independence is often referred to as Bayes net assumption.
- The Bayes net assumption
- Every variable in a Bayes net is conditionally independent of its non-descendants, given its parents.
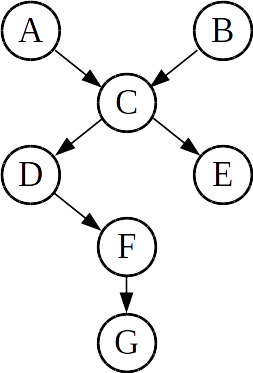
For example, consider the Bayes net shown below:
In this net, variable D has
- one parent (C),
- three ancestors (A, B, and C),
- two descendants (F and G), and
- 4 non-descendants (A, B, C, and E).
Then, we could say (for example) that
- D is conditionally independent of A given C: i.e. P(D|AC) = P(D|C)
- D is conditionally independent of E given C: i.e. P(D|EC) = P(D|C)
Conceptually, we see that the arrow relation simply indicates dependency: each variable is only dependent on the value(s) of its parent(s).
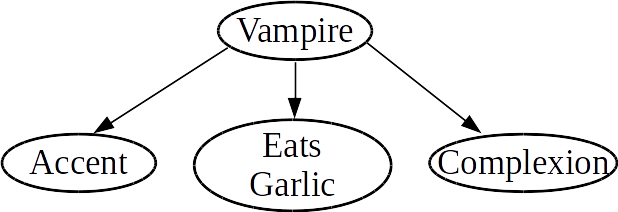
As a more concrete example, the following Bayes net encodes assumptions about the features of a subject versus its classification as a vampire or not:
In particular, the links in this graph inform us of the following:
- Every feature (accent, eats-garlic, and complexion) is conditionally independent of every other feature, given the classification as a vampire or not.
In a world with vampires, it would be crazy to claim that the individual features are independent: after all, if someone is a vampire, they are more likely to have particular traits. However, given that we know whether or not someone is a vampire, the features no longer depend on each other.
Part 1: Ancestors, descendants, and non-descendants
As warm up for this lab, you will now implement some basic functions that will help us throughout the remainder of the lab. As usual, we have supplied an API for lab 8 below, which gives you access to a lot of administrative functions for manipulating and interacting with Bayes nets, as well as a few other helper functions.
First, implement a function that takes in net (a BayesNet object) and var (a variable, as a string), and returns a set containing the ancestors of var in the network. This set should include the variable's parents, its parents' parents, etc.
def get_ancestors(net, var):
Next, implement a function that returns a set containing the descendants of the variable in the network. This set should include the variable's children, its children's children, etc.
def get_descendants(net, var):
Finally, implement a function that returns a set containing the non-descendants of the variable. Note that a variable is neither a descendant nor a non-descendant of itself.
def get_nondescendants(net, var):
Part 2: Probability
As a brief reminder, recall that there are three basic types of probabilities. Suppose our universe consists of five variables, A, B, C, D, and E. Then, the three types of probability associated with this universe are:
- Joint probability: Likelihood of a completely specified state of events, e.g. P(ABCDE)
- Marginal probability: Likelihood of an incompletely specified state of events, e.g. P(ACD) or P(E)
- Conditional probability: Likelihood of an event given some known information, e.g. P(A|C) or P(DE|AB)
When discussing probability, the hypothesis is the event or set of events whose likelihood we are interested in evaluating, and the givens are the event or events upon which we're conditioning the hypothesis. In other words,
- for a joint or marginal probability, we are interested in P(hypothesis)
- for a conditional probability, we are interested in P(hypothesis | givens)
In this lab, hypotheses and givens are expressed as dicts assigning variables to values. For example, P(A=False | B=True, C=False) is represented as the two dicts:
hypothesis = {'A': False}
givens = {'B': True, 'C': False}
The probability flowchart may be useful as a reference for manipulating probabilities.
Simplifying probability expressions
Before we start calculating probabilities, write a helper function that simplifies a probability expression using the independence assumption encoded in the Bayes net. This function will take in
- net, a BayesNet object
- var, a single Bayes net variable as a string
- givens, a dictionary mapping variables to assigned values in the net
and it will return another dictionary which is the simplified version of givens as allowed by the Bayes net assumption.
def simplify_givens(net, var, givens):
In other words,
- If all parents of var are given, and no descendants of var are given, simplify_givens should return a new dictionary of givens with var's non-descendants (except parents) removed.
- Otherwise, if not all the parents of var are given, or if the givens include one or more descendants of var, the function should simply return the original givens.
In either case, the function should not modify the original givens.
Hint: The set method .issubset may be useful here.
Looking up probabilities in a Bayes net
Now, we will implement a function that looks up probabilities in the net's conditional probability tables. This function takes in three arguments:
- net, a BayesNet object
- hypothesis, a dictionary mapping variables to values.
- givens, a dictionary mapping variables to assigned values. If this argument is None, the probability to look up is not conditioned on anything.
def probability_lookup(net, hypothesis, givens=None):
If the probability of the hypothesis variable can be looked up directly in the network's probability tables, or if its given variables can be simplified (with simplify_givens) to a form that can be looked up directly, return it. Otherwise, raise the exception LookupError.
Note that the function net.get_probability will raise a ValueError if the provided hypothesis contains multiple variables, or if the provided givens do not contain exactly the parents of the hypothesis' variable. You may want to use a try/except block to catch this error. We will handle multiple variable hypotheses in later functions.
(For a refresher on how to handle exceptions, see the appendix in Lab 5.)
Computing probabilities
Now we will implement functions that actually compute different types of probabilities. We will start by defining functions that can compute joint, marginal, and conditional probabilities; then we will generalize by implementing a single probability function.
Joint probability
Given net (a BayesNet object) and hypothesis (a dictionary mapping variables in the network to values), compute its joint probability:
def probability_joint(net, hypothesis):
For example to compute the joint probability P(A=True, B=False, C=False), one could call probability_joint(net, {"A": True, "B": False, "C": False}).
To compute the joint probability for a Bayes net, you can use the chain rule to split up the probability into a product of conditional probability values produced by probability_lookup. Hint: We can use the Bayes net Assumption to our advantage. When we expand using the chain rule, how can we order the variables to ensure that we can use probability_lookup for each term?
You may assume that the hypothesis represents a valid joint probability (that is, contains every variable in the Bayes net).
Marginal probability
Recall that a marginal probability can be represented as a sum of joint probabilities. You should implement probability_marginal (which takes in the same arguments as probability_joint) to compute the marginal probability as a sum of joint probabilities produced by probability_joint:
def probability_marginal(net, hypothesis):
For example, if there are two variables in the system, P(A=True) = P(A=True, B=True) + P(A=True, B=False).
Hint 1: The BayesNet method net.combinations may be useful.
Hint 2: If you are not passing every test for this function, consider the order in which you are expanding using the chain rule.
Conditional probability
Some conditional probabilities can be looked up directly in the Bayes net using probability_lookup. The rest, however, can be computed as ratios of marginal probabilities.
Implement probability_conditional, which takes in the same arguments as probability_marginal plus the addition of an optional givens dictionary mapping variables to values.
def probability_conditional(net, hypothesis, givens=None):
Note that if givens is None, the "conditional" probability is really just a marginal or joint probability.
Hint 1: To combine two dictionaries d1 and d2 to form a third dict d3, you can use d3 = dict(d1, **d2). (But note that if a key exists in both d1 and d2, the resulting dict d3 will only include the key's value from d2.)
Hint 2: There are a few nuanced edge cases to consider for a conditional probability. For example, in general, what is P(A=True|A=False)?
Tying it all together
Use all of the above types of probability to produce a function that can compute any probability expression in terms of the Bayes net parameters. This function takes in the same arguments as probability_conditional:
def probability(net, hypothesis, givens=None):
Part 3: Counting Parameters
Encoded in every Bayes net is a set of independence assumptions for the variables contained within. In general, knowing information about variables allows us to make more informed choices when computing probabilities. In particular, with these independence assumptions, we are able to drastically decrease the amount of information we need to store while still retaining the ability to compute any joint probability within the net.
Implement a function that takes in a single argument net (a BayesNet object), and returns the number of parameters in the network: that is, the minimum number of entries that must be stored in the network's probability tables in order to fully define all joint probabilities. Do not assume that the variables are boolean; any variable can take on an arbitrary number of values.
def number_of_parameters(net):
Python hint: The helper function product, defined in the API section, may be helpful here.
Conceptual hint: Consider variable C from the Bayes net above. Its two parents are A and B. Suppose each variable has three values in its domain. Then, the conditional probability table for C would look like this:
| A | B | P(C=c1 | A,B) | P(C=c2 | A,B) |
|---|---|---|---|
| a1 | b1 | # | # |
| a1 | b2 | # | # |
| a1 | b3 | # | # |
| a2 | b1 | # | # |
| a2 | b2 | # | # |
| a2 | b3 | # | # |
| a3 | b1 | # | # |
| a3 | b2 | # | # |
| a3 | b3 | # | # |
Questions to consider:
- How many parameters (represented by "#") are in the table? Why?
- Why don't we need a column for P(C=c3 | A,B)?
- How would this table change if...
- ...A were boolean?
- ...A had 5 values instead of 3?
- ...C had 5 values instead of 3?
- ...C had only one parent?
- ...C had a third parent, D?
If you're still having trouble with this section, we strongly recommend coming to office hours to discuss it with a TA, or other students!
Part 4: Independence
Lastly, we will write two functions that check for variable independence.
The first such function that you should implement is is_independent, which checks if two variables are numerically independent. This function takes in four arguments,
- net, a BayesNet object
- var1, a variable in the Bayes net
- var2, a variable in the Bayes net
- givens, a dictionary mapping variables to values; possibly None
returning True if var1 and var2 are independent.
def is_independent(net, var1, var2, givens=None):
If givens is None, this function checks if var1 and var2 are marginally independent. Otherwise, this function checks if var1 and var2 are conditionally independent given givens.
Hint: The helper function approx_equal may be useful for comparing probabilities.
Recall that variables can be independent either because of the topology of the network (structural independence), or because of their conditional probability table entries (numerical independence). In general, to determine variable independence, it is sufficient to check only numerical independence, because variables that are structurally independent are guaranteed to also be numerically independent. In other words, you can implement this function by computing and comparing probabilities, without considering d-separation.
Now, implement a function that checks for structural independence. This function takes in the same arguments as is_independent, and has the same return type.
def is_structurally_independent(net, var1, var2, givens=None):
You should use d-separation to determine whether var1 and var2 are independent, based solely on the structure of the Bayes net. This function should not consider numerical independence.
Lab 8 API
As usual, we have supplied an API for lab 8, which gives you access to a lot of administrative functions for manipulating and interacting with Bayes nets, as well as a few other helper functions.
Getting information from a BayesNet
The class BayesNet defines fields and methods for interacting with a Bayes network. To get some information from a BayesNet object, we supply the following methods:
- get_variables()
- Returns a list of all variables in the Bayes net.
- get_parents(var)
- Returns the set of variables that are the parents of var.
- get_children(var)
- Returns the set of variables that are the children of var.
- get_domain(var)
- Returns the domain of the variable. For example, if the variable is boolean, the function will return (False, True).
- is_neighbor(var1, var2)
- Returns True if var1 and var2 are directly connected by an edge in the Bayes net, otherwise returns False. In other words, returns True exactly when var1 is a parent of var2 or var2 is a parent of var1.
- find_path(start_var, goal_var)
- Performs breadth-first search (BFS) to find a path from start_var to goal_var. Returns path as a list of nodes (variables), or None if no path was found.
- get_probability(hypothesis, parents_vals=None, infer_missing=True)
- Given hypothesis (a singleton dictionary mapping a variable to its value) and parents_vals (a dictionary mapping all of the hypothesis variable's parents to values), looks up and returns a probability in the network's conditional probability tables. If infer_missing is True, the function will try to infer missing entries in the table using the fact that certain probabilities must sum to one.
- Requires that hypothesis has exactly one variable and that parents_vals's keys are exactly the parents of the hypothesis variable; if either condition isn't met, raises a ValueError.
- If the hypothesis variable does not exist in the network, or the value cannot be appropriately located in the conditional probability tables of the net, raises a LookupError.
- Example: Suppose net is a BayesNet instance with three boolean variables A, B, and C, with C the child of A and B. To look up P(C = True | A=False, B=False), you can call net.get_probability({"C" : True}, {"A": False, "B" : False}).
To view the structure of a BayesNet, you can print its variables and connections directly using the print statement.
To print a conditional probability table:
- CPT_print(var=None)
- Pretty-prints the Bayes net's conditional probability table for var (a variable in the net). If var is not specified, prints every conditional probability table in the net.
Iterating over a BayesNet
- topological_sort()
- Returns an ordered list of all variables such that each variable comes after all its parents.
- combinations(variables, constant_bindings=None)
- Given variables (a list of variables), and constant_bindings (a dictionary mapping variables to constant values), returns a list of dictionaries, each of which is a possible binding of variables, mapping variables to values. Each binding dictionary also includes the entries in constant_bindings, if specified.
- Example: If your Bayes net net has three boolean variables A, B, and C, calling net.combinations(['A','B','C']) will return a list of eight dictionaries indicating possible bindings for A, B, and C:
- {'A': False, 'B': False, 'C': False}
- {'A': False, 'B': False, 'C': True}
- {'A': False, 'B': True, 'C': False}
- {'A': False, 'B': True, 'C': True}
- {'A': True, 'B': False, 'C': False}
- ...
- {'A': True, 'B': True, 'C': True}
- Example: Passing constant_bindings = {'D': False, 'E': True} as an argument in the above example would include the entries {'D': False, 'E': True} in every one of the above eight bindings. On the other hand, passing constant_bindings = {'C': True} as an argument would result in only four bindings, each including the entry {'C': True}.
Creating or modifying a BayesNet
The following methods will allow you to create or modify a BayesNet instance.
- subnet(subnet_variables)
- Given subnet_variables (a list of variables in the net), returns a new BayesNet that is a subnet of this one. The new net includes the specified variables and any edges that exist between them in the original Bayes net. Ignores any specified variables that aren't in the original Bayes net.
- link(var_parent, var_child)
- Adds a directed edge from var_parent to var_child, then returns the modified Bayes net. If the edge already exists, this function does nothing, and returns the Bayes net.
- make_bidirectional()
- Adds edges so that all original edges effectively become bi-directional. Returns the modified Bayes net.
- remove_variable(var)
- Removes var from the Bayes net and deletes all edges to and from var. If var is not a variable in the Bayes net, does nothing. Returns the Bayes net.
Helper functions
We also provide a couple of helper functions that you may use directly in your lab8.py file:
- approx_equal(a, b, epsilon=0.0000000001)
- Returns True if two numbers a and b are approximately equal (within some margin epsilon), otherwise False.
- Example: approx_equal(0.4999999999999999, 0.5) --> True
- product(factors)
- Computes the product of a list of numbers, similar to the Python built-in function sum.
- Example: product([1,2,3,4]) --> 24
At this point, we strongly recommend reading the API again: there are several methods there that will likely be of use.
The following set methods may be useful:
- set1.update(set2): Update set1 with the union of itself and set2. (This is basically the set equivalent of list.extend.)
- set1.intersection(set2): Return the intersection of set1 and set2 as a new set.
Survey
Please answer these questions at the bottom of your lab file:
- NAME: What is your name? (string)
- COLLABORATORS: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)
- HOW_MANY_HOURS_THIS_LAB_TOOK: Approximately how many hours did you spend on this lab? (number or string)
- WHAT_I_FOUND_INTERESTING: Which parts of this lab, if any, did you find interesting? (string)
- WHAT_I_FOUND_BORING: Which parts of this lab, if any, did you find boring or tedious? (string)
- (optional) SUGGESTIONS: What specific changes would you recommend, if any, to improve this lab for future years? (string)
(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)
When you're done, run the online tester to submit your code.