Lab 5: Bayes Nets

From 6.034 Wiki

Revision as of 03:29, 13 November 2017 by Jb16 (Talk | contribs)

(diff) ←Older revision | Current revision (diff) | Newer revision→ (diff)

This lab has not yet been released. It may change between now and the release time, and may contain inaccurate or misleading directions. You will certainly need to download the code again once it is released.

The world is an uncertain place

So far in 6.034, we have discussed various machine learning methods that are used to classify data in different ways. Such methods have included k-nearest neighbors, support vector machines, and neural networks. These machine learning algorithms train on and predict classifications for data points that have definitive features, such as "height", "likes-garlic", or more mathematically abstract features like numbers x and y.

Unfortunately, the world is not so cut-and-dried. Often, we deal with features that may exist, values that fall somewhere within a distribution, or events that happen with some likelihood. As such, in this lab, we will be exploring the world of probability as well as Bayesian networks which encode certain assumptions in probability.

Bayesian Networks encode independence assumptions

As described in lecture and recitation, events might be marginally or conditionally independent.

A and B are said to be marginally independent when

A is said to be conditionally independent of B given C when

A Bayesian Network (also known as a Bayes Net) is a graphical model that encodes assumptions of conditional independence between certain events (variables). This assumption of conditional independence is often referred to as Bayes net assumption.

The Bayes net assumption: Every variable in a Bayes net is conditionally independent of its non-descendants, given its parents.

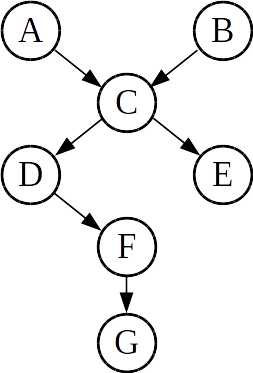
For example, consider the Bayes net shown below:

In this net, variable D has

one parent (C),
three ancestors (A, B, and C),
two descendants (F and G), and
4 non-descendants (A, B, C, and E).

Then, we could say (for example) that

D is conditionally independent of A given C: i.e. P(D|AC) = P(D|C)
D is conditionally independent of E given C: i.e. P(D|EC) = P(D|C)

Conceptually, we see that the arrow relation simply indicates dependency: each variable is only dependent on the value(s) of its parent(s).

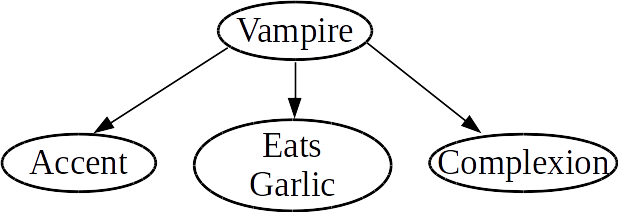
As a more concrete example, the following Bayes net encodes assumptions about the features of a subject versus its classification as a vampire or not:

In particular, the links in this graph inform us of the following:

Every feature (accent, eats-garlic, and complexion) is conditionally independent of every feature, given the classification as a vampire or not.

In a world with vampires, it would be crazy to claim that the individual features are independent: after all, if someone is a vampire, they are more likely to have particular traits. However, given that we know whether or not someone is a vampire, the features no longer depend on each other.

Lab 8 API

As usual, we have supplied an API for lab 8, which gives you access to a lot of administrative functions for manipulating and interacting with Bayes nets, as well as a few other helper functions. If you're confused about some of the nomenclature, don't worry! You can always read ahead and then come back to reference the API when necessary.

Getting information from a BayesNet

net.get_variables(): Returns a list of all variables in the Bayes net.
net.get_parents(var): Returns the set of variables that are the parents of var.
net.get_children(var): Returns the set of variables that are the children of var.
net.get_domain(var): Returns the domain of the variable. For example, if the variable is boolean, the function will return (False, True).
net.is_neighbor(var1, var2): Returns True if var1 and var2 are directly connected by an edge in the Bayes net, otherwise returns False. In other words, returns True just if var1 is a parent of var2, or var2 is a parent of var1.
net.get_probability(hypothesis, parents_vals=None, infer_missing=True): Given the value of a variable and all its parents, looks up and returns a probability in the network's conditional probability tables. For example, if A, B, C are boolean variables in a particular network, and C is the child of A and B; you can look up P(C = True | A=False, B=False) using net.get_probability({"C" : True}, {"A": False, "B" : False}). If infer_missing is True, the function will try to infer missing entries in the table using the fact that certain probabilities must sum to one. Note that get_probability may raise a ValueError or LookupError if it is unable to find the requested probability in the network's conditional probability tables.
net.find_path(start_var, goal_var): Performs breadth-first search (BFS) to find a path from start_var to goal_var. Returns path as a list of nodes (variables), or None if no path was found.

To view the structure of a BayesNet, you can print its variables and connections directly using print net.

To print a conditional probability table: net.CPT_print(var=None): Pretty-prints the Bayes net's conditional probability table for var. If var is not specified, prints every conditional probability table in the net.

Iterating over a BayesNet

net.topological_sort(): Returns an ordered list of all variables such that each variable comes after all its parents.

net.combinations(variables, constant_bindings=None): Given a list of variables, returns a list of every possible binding of those variables. For example, if you have three boolean variables "A", "B", "C", this function will return a list of eight possible bindings :

{'A': False, 'B': False, 'C': False}
{'A': False, 'B': False, 'C': True}
{'A': False, 'B': True, 'C': False}
{'A': False, 'B': True, 'C': True}
{'A': True, 'B': False, 'C': False}
…
{'A': True, 'B': True, 'C': True}

Each binding in the list will also include the entries in constant_bindings, if specified. For example, passing constant_bindings = {'D': False, 'E': True} as an argument would include the entries {'D': False, 'E': True} in every one of the above eight bindings. Passing constant_bindings = {'C': True} as an argument would result in only four bindings, each including the entry {'C': True}.

Debugging note: If net.combinations is returning duplicate entries, you can fix the problem by either not including any variables from variables in constant_bindings, or by updating your bayes_api.py. There was some unspecified behavior in the function, which we resolved shortly after the 2016 release of the lab.

Creating or modifying a BayesNet

We predict that you will only require the following four methods:

net.subnet(subnet_variables): Returns a new BayesNet that is a subnet of this one. The new net includes the specified variables and any edges that exist between them in the original Bayes net. Ignores any specified variables that aren't in the original Bayes net.
net.link(var_parent, var_child): Adds a directed edge from var_parent to var_child, then returns the Bayes net. (If the edge already exists, this function simply returns the Bayes net.)
net.make_bidirectional(): Adds edges so that all original edges effectively become bi-directional. Returns the Bayes net.
net.remove_variable(var): Removes var from the Bayes net and deletes all edges to/from var. (If var is not a variable in the Bayes net, does nothing.) Returns the Bayes net.

Helper functions

approx_equal(a, b, epsilon=0.0000000001): Returns True if two numbers a and b are approximately equal (within some margin epsilon), otherwise False.

Sample usage: approx_equal(0.4999999999999999, 0.5) -> True

product(factors): Computes the product of a list of numbers, similar to the Python built-in function sum

Part 1: Ancestors, descendants, and non-descendants

As warm up for this lab, you will now implement some basic functions that will help us throughout the remainder of the lab.

First, implement a function that takes in net (a BayesNet object) and var (a variable, as a string), and returns a set containing the ancestors of var in the network. This set should include the variable's parents, its parents' parents, etc.

def get_ancestors(net, var):

Next, implement a function that returns a set containing the descendants of the variable in the network. This set should include the variable's children, its children's children, etc.

def get_descendants(net, var):

Finally, implement a function that returns a set containing the non-descendants of the variable. Note that a variable is neither a descendant nor a non-descendant of itself.

def get_nondescendants(net, var):

Part 2: Probability

As a brief reminder, recall that there are three basic types of probabilities. Suppose our universe consists of five variables, A, B, C, D, and E. Then, the three types of probability associated with this universe are:

Joint probability: Likelihood of a completely specified state of events, e.g. P(ABCDE)
Marginal probability: Likelihood of an incompletely specified state of events, e.g. P(ACD) or P(E)
Conditional probability: Likelihood of an event given some known information, e.g. P(A|C) or P(DE|AB)

When discussing probability, the hypothesis is the event or set of events whose likelihood we are interested in evaluating, and the givens are the event or events upon which we're conditioning the hypothesis. In other words,

for a joint or marginal probability, we are interested in P(hypothesis)
for a conditional probability, we are interested in P(hypothesis | givens)

In this lab, hypotheses and givens are expressed as dicts assigning variables to values. For example, P(A=False | B=True, C=False) is represented as the two dicts:

hypothesis = {'A': False}
givens = {'B': True, 'C': False}

The probability flowchart may be useful as a reference for manipulating probabilities.

Simplifying probability expressions

Before we start calculating probabilities, write a helper function that simplifies a probability expression using the independence assumption encoded in the Bayes net. This function will take in

net, a BayesNet object
var, a single bayes net variable as a string
givens, a dictionary mapping variables to assigned values in the net

and it will return another dictionary which is the simplified version of givens as allowed by the Bayes net assumption.

def simplify_givens(net, var, givens):

In other words,

If all parents of var are given, and no descendants of var are given, simplify_givens should return a new dictionary of givens with var's non-descendants (except parents) removed.
Otherwise, if not all the parents of var are given, or if the givens include one or more descendants of var, the function should simply return the original givens.

In either case, the function should not modify the original givens.

Hint: The set method .issubset may be useful here.

Looking up probabilities in a Bayes net

Now, we will implement a function that looks up probabilities in the net's conditional probability tables. This function takes in three arguments:

net, a BayesNet object
hypothesis, a dictionary mapping variables to values.
givens, a dictionary mapping variables to assigned values. If this argument is None, the probability to look up is not conditioned on anything.

def probability_lookup(net, hypothesis, givens=None):

If the probability of the hypothesis variable can be looked up directly in the network's probability tables, or if its given variables can be simplified (with simplify_givens) to a form that can be looked up directly, return it. Otherwise, raise the exception LookupError.

Note that net.get_probability will raise a ValueError if the hypothesis contains multiple variables, or if the givens do not contain exactly the parents of the hypothesis' variable. You may want to use a try/except block to catch this error.

(For a refresher on how to handle exceptions, see the appendix in Lab 5.)

Computing probabilities

Now we will implement functions that actually compute different types of probabilities. We will start by defining functions that can compute joint, marginal, and conditional probabilities; then we will generalize by implementing a single probability function.

Joint probability

Given net (a BayesNet object) and hypothesis (a dictionary mapping variables in the network to values), compute its joint probability:

def probability_joint(net, hypothesis):

For example to compute the joint probability P(A=True, B=False, C=False), one could call probability_joint(net, {"A": True, "B": False, "C": False}).

To compute the joint probability for a Bayes net, you can use the chain rule to split up the probability into a product of conditional probability values produced by probability_lookup.

You may assume that the hypothesis represents a valid joint probability (that is, contains every variable in the Bayes net).

Marginal probability

Recall that a marginal probability can be represented as a sum of joint probabilities. You should implement probability_marginal (which takes in the same arguments as probability_joint) to compute the marginal probability as a sum of joint probabilities produced by probability_joint:

def probability_marginal(net, hypothesis):

For example, if there are three variables in the system, P(A=True) = P(A=True, B=True) + P(A=True, B=False).

Hint 1: The BayesNet method net.combinations may be useful.

Hint 2: To combine two dictionaries d1 and d2 to form a third dict d3, you can use d3 = dict(d1, **d2). (But note that if a key exists in both d1 and d2, the resulting dict d3 will only include the key's value from d2.)

Conditional probability

Some conditional probabilities can be looked up directly in the Bayes net using probability_lookup. The rest, however, can be computed as ratios of marginal probabilities.

Implement probability_conditional, which takes in the same arguments as probability_marginal plus the addition of an optional givens dictionary mapping variables to values.

def probability_conditional(net, hypothesis, givens=None):

Note that if givens is None, the "conditional" probability is really just a marginal or joint probability.

Tying it all together

Use all of the above types of probability to produce a function that can compute any probability expression in terms of the Bayes net parameters. This function takes in the same arguments as probability_conditional:

def probability(net, hypothesis, givens=None):

Part 3: Counting Parameters

Encoded in every Bayes net is a set of independence assumptions for the variables contained within. In general, knowing information about variables allows us to make more informed choices when computing probabilities. In particular, with these independence assumptions, we are able to drastically decrease the amount of information we need to store while still retaining the ability to compute any joint probability within the net.

Implement a function that takes in a single argument net (a BayesNet object), and returns the number of parameters in the network: that is, the minimum number of entries that must be stored in the network's probability tables in order to fully define all joint probabilities. Do not assume that the variables are boolean; any variable can take on an arbitrary number of values.

def number_of_parameters(net):

Python hint: The helper function product, defined in the API section, may be helpful here.

Conceptual hint: Consider variable C from the Bayes net above. Its two parents are A and B. Suppose each variable has three values in its domain. Then, the conditional probability table for C would look like this:

A	B	P(C=c1 \| A,B)	P(C=c2 \| A,B)
a1	b1	#	#
a1	b2	#	#
a1	b3	#	#
a2	b1	#	#
a2	b2	#	#
a2	b3	#	#
a3	b1	#	#
a3	b2	#	#
a3	b3	#	#

Questions to consider:

How many parameters (represented by "#") are in the table? Why?
Why don't we need a column for P(C=c3 | A,B)?
How would this table change if...
- ...A were boolean?
- ...A had 5 values instead of 3?
- ...C had 5 values instead of 3?
- ...C had only one parent?
- ...C had a third parent, D?

Part 4: Independence

Lastly, we will write two functions that check for variable independence.

The first such function that you should implement is is_independent, which checks if two variables are numerically independent. This function takes in four arguments,

net, a BayesNet object
var1, a variable in the Bayes net
var2, a variable in the Bayes net
givens, a dictionary mapping variables to values; possibly None

returning True if var1 and var2 are independent.

def is_independent(net, var1, var2, givens=None):

If givens is None, this function checks if var1 and var2 are marginally independent. Otherwise, this function checks if var1 and var2 are conditionally independent given givens.

Hint: The helper function approx_equal may be useful for comparing probabilities.

Recall that variables can be independent either because of the topology of the network (structural independence), or because of their conditional probability table entries (numerical independence). In general, to determine variable independence, it is sufficient to check only numerical independence, because variables that are structurally independent are guaranteed to also be numerically independent. In other words, you can implement this function by computing and comparing probabilities, without considering d-separation.

Now, implement a function that checks for structural independence. This function takes in the same arguments as is_independent, and has the same return type.

def is_structurally_independent(net, var1, var2, givens=None):

You should use d-separation to determine whether var1 and var2 are independent, based solely on the structure of the Bayes net. This function should not consider numerical independence.

The following set methods may be useful:

set1.update(set2): Update set1 with the union of itself and set2. (This is basically the set equivalent of list.extend.)
set1.intersection(set2): Return the intersection of set1 and set2 as a new set.

Survey

Please answer these questions at the bottom of your lab file:

NAME: What is your name? (string)

COLLABORATORS: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)

HOW_MANY_HOURS_THIS_LAB_TOOK: Approximately how many hours did you spend on this lab? (number or string)

WHAT_I_FOUND_INTERESTING: Which parts of this lab, if any, did you find interesting? (string)

WHAT_I_FOUND_BORING: Which parts of this lab, if any, did you find boring or tedious? (string)

(optional) SUGGESTIONS: What specific changes would you recommend, if any, to improve this lab for future years? (string)

(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)

When you're done, run the online tester to submit your code.