Lab 2: Games
From 6.034 Wiki
Contents
|
This lab is due by Thursday, September 24 at 10:00pm.
Before working on the lab, you will need to get the code. You can...
- Use Git on your computer: git clone username@athena.dialup.mit.edu:/mit/6.034/www/labs/fall2020/lab2
- Use Git on Athena: git clone /mit/6.034/www/labs/fall2020/lab2
- Download it as a ZIP file: http://web.mit.edu/6.034/www/labs/fall2020/lab2/lab2.zip
- View the files individually: http://web.mit.edu/6.034/www/labs/fall2020/lab2/
All of your answers belong in the main file lab2.py. To submit your lab to the test server, you will need to download your key.py file and put it in either your lab2 directory or its parent directory. You can also view all of your lab submissions and grades here.
Games and Adversarial search
This lab has two parts. In the first part of this lab, you'll work with the game Connect Four, writing methods to represent states of a Connect Four game as a game tree.
In the second part of this lab, you'll write subroutines for performing various search functions on a game tree, including
- depth-first search,
- ordinary minimax search,
- minimax search with alpha-beta pruning, and
- progressive deepening.
Part 1: Utility functions for playing Connect Four
Representing Connect Four as a game tree
Connect Four is a two-player game where players take turns dropping a token into a 6 x 7 grid. The first player to build a consecutive sequence of four of their own tokens wins the game. The sequence of four tokens can lie either horizontally, vertically, or diagonally. In this way, Connect Four is similar to other games you might know, such as Tic-tac-toe.
Stated more abstractly, Connect Four is a game where each player has seven possible moves in a turn, corresponding to the seven columns where the player can drop the piece (unless the column is full, in which case the player cannot move there).
We have provided an API for constructing and manipulating Connect Four boards. We suggest you take a look at the API now before getting started. For the first part of this lab, you will define subroutines that
- determine whether the game is over,
- generate a player's set of possible moves, and
- assign scores to boards.
These subroutines will provide the necessary definitions for treating Connect Four boards as states in a game tree, which will be useful in the second half of this lab.
Game over
Return True if the game is over, otherwise False. The game is over when the board contains a chain of length 4 (or longer), or all columns are full.
def is_game_over_connectfour(board) :
Generating all possible moves
Return a list of boards representing the game state that can result by making a single move in any legal column.
First, you should check in advance if the game is already over and return the empty list if so. If the game is not over, then, at most, you can move in any of the seven columns. But you cannot legally move in a column if it's full, and so you should exclude those.
Note that these next-states that are generated should be the result of the current player playing a piece, which means that in each of the next-states, the other player is the "current" player because they have yet to make a move.
For each board in the list, board.prev_move_string() notes the column in which a piece was played (for debugging purposes).
Note: iterate over columns in increasing numerical order.
def next_boards_connectfour(board) :
Assigning points to the winner
Here, we'll define the final score of a Connect Four game that has been won. We'll return a score of 1000 if the maximizer has won, or -1000 if the minimizer has won. In case of a tie, return 0 instead. A tie occurs when the entire board fills up but has no chains of 4 or more same-colored tokens.
Important subtlety regarding endgame scoring: We don't know if a game is over until we take the board and call is_game_over_connectfour(board) on it. The board represents the state of the game after the previous player moved, but before the current player has played. Hence, if the game is already over, it's because the previous player played the final move, ending the game. Therefore, if the game is over and someone has won, it's not the current player who has won, because it just became the current player's "turn"; instead, the previous player has won.
In short, although it is slightly counter-intuitive, the endgame scoring function should return -1000 for a winning board if the current player is the maximizer (because that means the minimizer played the winning move), and +1000 if the current player is the minimizer.
def endgame_score_connectfour(board, is_current_player_maximizer) :
Win already!
The previous endgame_score_connectfour function has the drawback that it doesn't reward players for winning sooner, since all winning states have the same value. Therefore, it doesn't encourage the computer to win as fast as possible the way a human would. To remedy this, write a score function that rewards players for winning sooner: that is, it should assign a better score to games that are won in fewer moves.
To retain consistency with your other endgame scoring function, make sure you return a value with abs(score) >= 1000 to indicate that someone has won. (In this lab, scores of magnitude 1000 or greater will correspond to winning game states, whereas scores of magnitude < 1000 will correspond to games that have not yet been won.)
def endgame_score_connectfour_faster(board, is_current_player_maximizer) :
Hint: you can use board.count_pieces() to help determine how long the game has gone on.
A heuristic for ConnectFour boards
In practice, it is infeasible to search all the way to the leaves of the game tree in order to find a score. (Imagine ranking opening chess moves by whether they are automatic wins/losses for perfect play.)
Instead, here we will define a heuristic for estimating the "goodness" of a state --- specifically the goodness of a Connect Four board --- and use that in place of an endgame scoring function when we want to stop evaluation before reaching the end of the game.
In practice, designing accurate heuristics greatly assists the decision making of strong game-playing AIs. Developing a good heuristic is a matter of design: there are many possible strategies and ways of measuring/defining the goodness of a state; for the purposes of this lab, you only need to define a scoring function that gives better scores for obviously stronger Connect Four positions.
def heuristic_connectfour(board, is_current_player_maximizer) :
As a hint, much of the information about the goodness of a state concerns the number and length of both players' chains. And, just to remain consistent with endgame scores, the absolute value of the heuristic scores should be scaled to be less than 1000. As before, the returned score will be negated depending on whether the current player is the maximizer.
For example, you might return:
- 500 for a board in which the maximizer is doing much better
- 10 for a board in which the maximizer is doing only slightly better
- 0 for a board in which neither player seems to have an advantage
- -10 for a board in which the minimizer is doing slightly better
- ...and so on.
On to Abstract Game States
Transforming the game into an abstract game state will allow us to explore the evolution of ConnectFour and other game states through the lens of minimax search algorithms.
To define the rules and starting state of the game Connect Four, we can pass some of the functions you wrote above to the AbstractGameState constructor. In lab3.py, you can find two examples of an AbstractGameState object representing a Connect Four game:
# This AbstractGameState represents a new ConnectFourBoard, before the game has started:
state_starting_connectfour = AbstractGameState(snapshot = ConnectFourBoard(),
is_game_over_fn = is_game_over_connectfour,
generate_next_states_fn = next_boards_connectfour,
endgame_score_fn = endgame_score_connectfour_faster)
# This AbstractGameState represents the ConnectFourBoard "NEARLY_OVER" from boards.py:
state_NEARLY_OVER = AbstractGameState(snapshot = NEARLY_OVER,
is_game_over_fn = is_game_over_connectfour,
generate_next_states_fn = next_boards_connectfour,
endgame_score_fn = endgame_score_connectfour_faster)
Part 2: Searching a game tree
This part of the lab involves writing search functions on game trees made out of AbstractGameStates. The utility functions from Part 1 allow you to construct an AbstractGameState out of Connect Four boards, but the methods you write will work on other games as well.
Abstract game states have methods for:
- Checking whether the game is over (state.is_game_over()).
- Generating a list of the resulting game state for each legal move (state.generate_next_states())
- Returning an object representing a current snapshot of the game.
- Computing the endgame score of a state, if the game is over.
There are other methods and attributes as well; for a more complete list, see the API.
About sample game states: To help you test out your search algorithms in this section, we provide several sample game states for Connect Four in your lab3.py file. There are also print statements that you can uncomment to see examples of what each algorithm returns. You can also print the current snapshot of an AbstractGameState object to get intuition for the current state of the game.
Cooperative depth-first search
To start, we will see what non-adversarial search looks like. In particular, all of the search algorithms we've studied so far have been non-adversarial because they assume that you have the same goal at each level of the tree (rather than players taking turns to move toward opposing goals). Imagine that both players are trying to collaboratively find the path that leads to the highest score. We will search the tree in depth-first search order to find the path leading to the highest score.
Your task will be to implement this non-adversarial DFS maximizing search. It should be very similar to the DFS search from the previous lab, with two key differences:
- This search should not terminate once it has found a path to a "goal." Instead, the search should explore all possible paths to all leaves (end-game states), just in a depth-first order. After finding all such paths, the best one (the one with the largest end-game state score) is chosen and returned.
- This algorithm should not only return the best path, but also the score of that path (the score of the end-game state at the end of that path) and the number of static evaluations that were computed. This will be explained in detail below.
We will use this search as a jumping-off point for the remainder of this lab. After implementing this DFS maximizing search, we will start building other algorithms on top of it.
Implement the function dfs_maximizing, which takes as input a state of type AbstractGameState and should return a tuple containing, in order,
- the best path: a list of AbstractGameStates illustrating the sequence of moves necessary to achieve the highest score, starting with the initial state;
- the score value of the leaf node: a number; and
- the number of static evaluations you performed during search: a number. (Remember that a static evaluation can happen by calculating an endgame score or a heuristic score, but not by recursing on a node's children.)
def dfs_maximizing(state) :
In case two moves have the same score, break ties by preferring earlier branches to later branches (i.e. if two moves have the same score, prefer the earlier one).
Debugging hints:
- You can use the method pretty_print_dfs_type(result) to print the result from dfs_maximizing (or any of the later minimax search functions) in a human-readable way.
- You can also use the built-in print to print ConnectFourBoard and AbstractGameState objects.
Minimax search with endgame scores only
Find the minimax path. The boolean argument maximize determines whether the current player is the maximizer or not. This function should have the same return type as dfs; that is, it should return a tuple containing the minimax path, the minimax score, and the number of static evaluations performed during search.
def minimax_endgame_search(state, maximize=True) :
In case two moves have the same minimax score, break ties by preferring earlier branches to later branches (i.e. if two moves have the same minimax score, prefer the earlier one.)
Important clarification: Either the maximizer or the minimizer may make the first move, so to determine which player is maximizing, don't look at the game state itself --- look at the maximize argument to the search function. Additionally, you might find some methods from the API helpful, such as state.get_endgame_score(is_current_player_maximizer=True).
As you move through the minimax variations, a helpful hint might be to consider how each of these functions are similar to one another!
If you want to review how minimax works, here are a couple resources:
Minimax with heuristic and endgame scores
The previous version of minimax that you wrote could only handle endgame states. Now we'll define minimax search that can search to any shallower depth, using a heuristic score instead of an endgame score for states that are not endgame states.
- What is depth?
- We define depth to be how many ancestors a node has: at the root of a tree, the depth is 0; one level down, the depth is 1, and so on. Hence, when we refer to a depth limit of (say) 3, that means the algorithm should look ahead by up to 3 levels, including the level at depth = 3.
Define minimax search that can search up to any specified depth in the tree. Given a state, your algorithm should:
- Evaluate the state using the endgame scoring function (state.get_endgame_score) if the state is an endgame state.
- Evaluate the board using the heuristic_fn if the state is at the limit of search.
- Or otherwise, generate all subsequent moves, recurse on them, and amalgamate the results.
- Break ties by preferring earlier branches to later branches (i.e. if two moves have the same minimax score, prefer the earlier one.)
This function should have the same return type as the other search methods above. When counting evaluations, you should include both the number of endgame score evaluations and the number of heuristic score evaluations.
def minimax_search(state, heuristic_fn=always_zero, depth_limit=INF, maximize=True) :
By default, minimax_search uses the heuristic function always_zero(state, maximize=True), which returns a score of zero for any board.
Important Note: The scoring functions state.get_endgame_score(is_current_player_maximizer=True) and heuristic_fn(board, maximize=True) differ in three key ways:
- Endgame scores are used only for leaf nodes of the game tree; heuristic functions are used only for non-leaf nodes.
- Because endgame score is an objective measure of endgame value, it is a method of the AbstractGameState; in contrast, heuristic_fn is an argument of the search function, and varies depending on the priorities of the player.
- The method .get_endgame_score applies to Abstract Game State objects; in contrast, heuristic functions apply to the underlying snapshot objects. For example, the heuristic_connectfour function (defined above) takes a ConnectFourBoard object as its main argument.
Both state.get_endgame_score and heuristic_fn take in a boolean argument is_current_player_maximizer. For state.get_endgame_score, the default value for this argument is True.
To better visualize why looking deeper into a game is so important, uncomment and try minimax_search on "BOARD_UHOH".
Minimax with alpha-beta optimization
Perform alpha-beta pruning, with the same return type as minimax_search:
def minimax_search_alphabeta(state, alpha=-INF, beta=INF, heuristic_fn=always_zero, depth_limit=INF, maximize=True) :
If you want to review how alpha-beta pruning works, here are a few resources:
- Dylan's alpha-beta demo
- Chapter 6 of the textbook
- Prof. Bob Berwick's notes on minimax and alpha-beta
Just for fun: Play against your AI!
When you're done implementing minimax_search_alphabeta, you can run play_game.py to play Connect Four against your AI!
Use progressive deepening to return anytime values
In this final section, you'll write a progressive deepening algorithm which uses minimax with alpha-beta pruning to search progressively deeper into the tree until time runs out. The arguments to progressive_deepening are identical to minimax_search, but the return type is an AnytimeValue object. You can declare a new AnytimeValue object like any other object. For example, anytime_value = AnytimeValue().
AnytimeValue objects are simple, with the following methods:
- .set_value(val): sets the value to the val and stores val in the AnytimeValue's history
- .get_value(): returns the current value
- .pretty_print(): prints the AnytimeValue's history in human-readable format
You can code progressive deepening using a similar technique to the other search algorithms. Here, you'll make iterative calls to minimax_search_alphabeta, increasing the depth each time. But at each level when minimax_search_alphabeta returns a new value, store that most recent result using anytime_value.set_value(new_best_option).
def progressive_deepening(state, heuristic_fn=always_zero, depth_limit=INF, maximize=True) :
Debugging hints:
- Be sure to search all the way to the depth limit (as opposed to stopping at depth_limit - 1)
- Consider this question: What is the shallowest (smallest) depth you can search to while still obtaining useful information about which move to make?
Optional: Incorporate real time into your anytime algorithm!
The progressive deepening function you just implemented will continue to run until it reaches its depth limit, because it doesn't have the concept of a time limit. There are no tests for this section -- it's difficult to test timed algorithms because the performance will vary greatly from one machine to another -- but here are some instructions in case you'd like add a time limit to your progressive deepening algorithm.
def progressive_deepening(state, heuristic_fn=always_zero, depth_limit=INF, maximize=True, time_limit=INF)
- Add a time_limit parameter to the signature of your function, as shown above.
- Then, import and use a function such as time.time() to keep track of how much time has elapsed since your algorithm started running.
- At regular intervals (e.g. before progressing to the next level of progressive deepening), check whether time has run out by comparing the elapsed time to the permitted time_limit. If you want, you could even incorporate the time-limit checking into alpha-beta by passing the time_limit argument into your alpha-beta function.
- Try running your modified progressive_deepening function with a time limit (e.g. time_limit=15) and no depth limit (depth_limit=INF) and see what happens! You should observe that as you increase the time limit, progressive_deepening will have time to look further ahead in the game tree.
Part 3: Conceptual Questions
Here are a few multiple-choice questions to test your conceptual understanding of the material in this lab. For explanations of the answers, look near the bottom of tests.py
Fill in the answer to each question in ANSWER_i at the bottom of lab3.py. Each answer should be a string: '1', '2', '3', '4', or '5'.
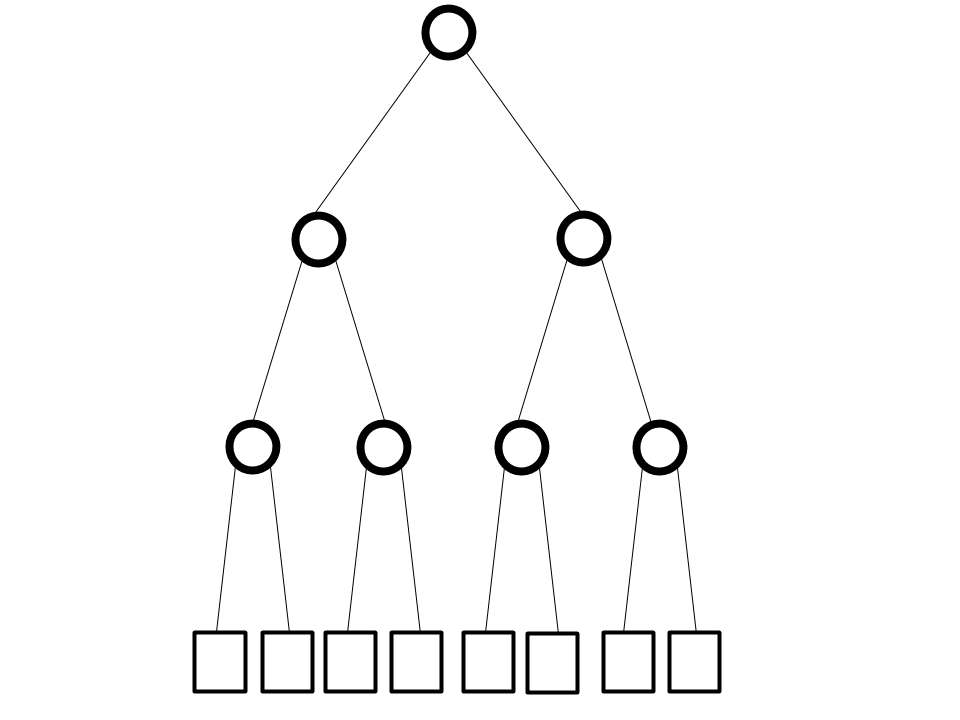
Questions 1-3 refer to a game tree shaped like the one below (i.e. a binary tree of depth three, with eight leaves). When answering the questions, consider all possible game trees of this shape:
Question 1: Suppose our game tree is of the above shape, and we are running endgame minimax search with no heuristic, and without alpha-beta pruning. Which of the following conditions will guarantee that we will not be required to examine all eight leaves of the tree?
- When the sequence of leaves generated by doing a depth-first traversal is monotonically decreasing, and the current player is MAX
- When the values of the leaves are randomly generated
- We will never have to examine all eight leaves, regardless of whose turn it is or what the values of the leaves are
- We will always have to examine all eight leaves, regardless of whose turn it is or what the values of the leaves are
- None of the above
Question 2: Suppose our game tree is of the above shape, and we are running endgame minimax search with alpha-beta pruning. Which of the following conditions will guarantee that we will not be required to examine all eight leaves of the tree?
- When the sequence of leaves generated by doing a depth-first traversal is monotonically decreasing, and the current player is MAX
- When the values of the leaves are randomly generated
- We will never have to examine all eight leaves, regardless of whose turn it is or what the values of the leaves are
- We will always have to examine all eight leaves, regardless of whose turn it is or what the values of the leaves are
- None of the above
Question 3: Suppose you just ran endgame minimax search with alpha-beta pruning (with depth_limit=INF and heuristic_fn=always_zero) on some game tree T of the above shape, but your algorithm didn't prune any leaves from T. You're unhappy with this result! You want your algorithm to prune some leaves! Which of the following changes to your alpha-beta search algorithm would likely increase the number of leaves pruned while searching T?
- Swap the order of the root node's children
- For each of the seven non-leaf nodes, randomly pick an order for the two children of that node
- Use a different, better heuristic_fn instead of always_zero
- Both 1 and 2
- All of 1, 2, and 3
Question 4: This question does not refer to the above tree; it could refer to any game tree. Suppose an adversary, Eve, knows the exact implementation of your alpha-beta search, as well as the static value (heuristic or endgame score) of every node in the game tree you're about to search. Before running your algorithm on a particular game tree, Eve may decide to reorder the children of any number of nodes in the tree. Being an adversary, Eve's intention is to order nodes so that your alpha-beta algorithm will prune as few leaves as possible. (Note Eve is not allowed to shear the tree -- i.e. change the parent of a node -- and Eve is not allowed to modify the tree once your algorithm has started running.)
With this in mind, which of the following is the best change you can make to your algorithm to maximize the number of nodes that you can expect to prune? In other words, how can you make Eve's efforts worthless? Note that Eve will also see any changes you make to your code and will have an opportunity to reorder the tree after you make your changes!
- Have your algorithm pick a random number n at the start of execution, then run alpha-beta on the game tree n times, averaging the results each time.
- Set heuristic_fn=always_zero, which means that the heuristic score for any node is zero.
- Set heuristic_fn=random_int, where random_int is a function that returns a random integer, regardless of game state.
- Set depth_limit to something tiny like 1 or 2, forcing your search to rely heavily on heuristics and not endgame scores.
- Instead of doing standard DFS search, have your algorithm explore the children of each node in a random order.
API
Throughout this lab, you can use the constant INF in lab3.py to represent infinity.
ConnectFourBoard
ConnectFourBoard is class for probing and manipulating the state of a Connect Four game. A ConnectFourBoard has players (represented by their name strings), and pieces. Players' pieces are represented by numbers: 1 denotes the first player's piece, 2 denotes the second player's piece, and 0 denotes an empty space in the board.
The dimensions of the board are stored as class attributes:
- num_rows
- The number of rows in the board (= 6).
- num_cols
- The number of columns in the board (= 7).
We provide methods for acquiring information about the pieces in the board:
- count_pieces(current_player=None)
- With no arguments, returns the total number of pieces on the board. Otherwise, returns the number of pieces owned by the current player (current_player = True) or by the other player (current_player = False).
- get_all_chains(current_player=None)
- With no arguments, returns a list of all maximal contiguous chains of pieces. (A chain is a sequence of pieces belonging to a single player, arranged either horizontally, vertically, or diagonally.) Each chain is a list of 1s (for pieces belonging to the player who moved first) or 2s (for pieces belonging to the player who moved second.) If current_player=True, returns only chains belonging to the current player. If current_player=False, returns only chains belonging to the other player.
- get_piece(col, row)
- Return the piece in the given column and row. The Connect Four board has seven columns and six rows. Return value is 1 (a piece owned by the first player), 2 (a piece owned by the second player), or 0 (if the space is empty).
You can also investigate or make moves in particular columns:
- is_column_full(col_number)
- Given an integer between 0 (leftmost column) and 6 (rightmost column), returns a boolean value representing whether the column is full of pieces or not.
- add_piece(col_number)
- Adds the current player's piece to the given column. This method does not modify the original board, but instead returns a new ConnectFourBoard object with the piece added. In the new board, the current player will have swapped.
- get_column_height(col_number)
- Return the number of pieces in the specified column. The returned value will be a number between 0 (no pieces in the column) and 6 (the column is full).
There are two players who are represented by their names (as strings). The names are entirely irrelevant, but names may make debugging more intuitive. Note: Player names do not determine which player is the maximizer and which player is the minimizer; those roles are attributes of the search algorithms, not the game itself.
- players
- The list of the players' names. The order will change so that the current player is always first in the list.
- get_player_name(n)
- Return the name of the player who moved first (n=1) or second (n=2) in this game.
Finally, you can make a copy of a board, in case you want to modify a copy without modifying the original:
- copy()
- Returns a (deep) copy of the board.
How chains of pieces are represented
Connect Four is built around chains of pieces; a chain is a sequence of a single player's pieces either horizontally, vertically, or diagonally. Here's an example of a board and the chains in it.
This is a completed Connect Four game between two players named Red Fish (who uses red pieces and moves first) and Blue Fish (who uses black pieces and moves second):
Python's printed representation of the board looks like this:
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 2 2 2 _ _ 1 1 1 1 2 1 _
Optionally, if you want to see how the board is encoded, you can find it in boards.py, defined as BOARD_REDFISH_WON_LESS_FAST.
If you call board.get_all_chains() with no arguments, it returns the following list:
[[1], [2, 2, 2], [1, 1, 1, 1], [2, 2], [2, 2]]
These are all the chains in the board:
- 1 has a piece by itself on the far right.
- 2 has a horizontal chain of three pieces.
- 1 has a horizontal chain of four pieces (Winning the game!).
- 2 has a vertical chain of two pieces.
- 2 has a diagonal chain of two pieces (in the "northwest" diagonal direction)
You can also call get_all_chains with a boolean argument, in which case it will return only chains belonging to the current player (True) or other player (False). For example in this case, since it would have been 2's turn if 1 hadn't already won, board.get_all_chains(True) returns:
[[2, 2, 2], [2, 2], [2, 2]]
which are the chains belonging to 2 in the complete list returned above.
AbstractGameState
AbstractGameState is a class which encodes the rules of a game and a snapshot of its current position. They are generic enough to encode the rules of any game that can be played with minimax.
AbstractGameState objects can be traversed like trees:
- generate_next_states()
- Get the children of this node in the game tree, returning a list of AbstractGameState objects corresponding to the result of each possible legal move. If there are no possible moves, return the empty list.
- is_game_over()
- Returns True if this is a leaf node in the game tree, otherwise False.
- get_endgame_score(is_current_player_maximizer=True)
- If this node is a leaf node (i.e. an endgame state), returns its final score. The score will be negated depending on whether the current player is a maximizer (default) or not. If this node is not a leaf node, throws an error.
You can also access an internal snapshot of the current game. This allows you to access game-specific details such as the number of pieces in a Connect Four board. The snapshot will also be helpful because heuristic score functions evaluate not the AbstractGameState object, but its snapshot of the current position. (This is an implementation difference between endgame scoring functions and heuristic scoring functions.)
- get_snapshot()
- Returns a snapshot of the current state of the game. Depending on the game, the type of the returned object may be different. For example, if the game is Connect Four, the snapshot will be a ConnectFourBoard object.
Finally, you may find the following methods useful when debugging:
- describe_previous_move()
- Returns a string representing how the current state was generated from its parent. For example, if the game is Connect Four, previous move strings look like "Put Player Two's piece in column 4."
- restart()
- Reset the game to the initial state. Returns the reset AbstractGameState object.
Survey
Please answer these questions at the bottom of your lab file:
- NAME: What is your name? (string)
- COLLABORATORS: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)
- HOW_MANY_HOURS_THIS_LAB_TOOK: Approximately how many hours did you spend on this lab? (number or string)
- WHAT_I_FOUND_INTERESTING: Which parts of this lab, if any, did you find interesting? (string)
- WHAT_I_FOUND_BORING: Which parts of this lab, if any, did you find boring or tedious? (string)
- (optional) SUGGESTIONS: What specific changes would you recommend, if any, to improve this lab for future years? (string)
(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)
When you're done, run the online tester to submit your code.
FAQ
Q: When I run the tester, I'm getting a weird error that looks like
AttributeError: 'AbstractGameState' object has no attribute 'get_all_chains'
or
AttributeError: 'AbstractGameState' object has no attribute 'board_array'
A: This happens when you try to call heuristic_fn on an AbstractGameState instead of on the underlying snapshot. A heuristic function only makes sense when it's tied to a particular game, not to any abstract game.