Lab 1: Search
From 6.034 Wiki
Contents |
This lab is due by Thursday, September 17 at 10:00pm.
Before working on the lab, you will need to get the code. You can...
- Use Git on your computer: git clone username@athena.dialup.mit.edu:/mit/6.034/www/labs/fall2020/lab1
- Use Git on Athena: git clone /mit/6.034/www/labs/fall2020/lab1
- Download it as a ZIP file: http://web.mit.edu/6.034/www/labs/fall2020/lab1/lab1.zip
- View the files individually: http://web.mit.edu/6.034/www/labs/fall2020/lab1/
All of your answers belong in the main file lab1.py. To submit your lab to the test server, you will need to download your key.py file and put it in either your lab1 directory or its parent directory. You can also view all of your lab submissions and grades here.
Python Advice
In this lab, you will undoubtedly need to sort Python lists during this lab (using either the in-place .sort method or sorted function). Python has built-in sorting functionality.
You will also need to know how to access particular elements in lists and dictionaries. For some portions of this lab, you may want to treat lists like either stacks or queues. However, you should not import other modules (such as collections.deque) for this purpose because they will confuse the tester.
Search Overview
The Agenda
Different search techniques explore nodes in different orders, and we will use a Python list that we will call an agenda (sometimes informally referred to as the queue) to keep track of nodes to be explored. The agenda has a front (or beginning or top), and a back (or end or bottom):
agenda = [front, ..., back]
We will often refer to putting things onto the front of the agenda. This means putting an item in the agenda's index-0 position. Similarly, putting an item at the back of the agenda means appending it to the end of the list.
In search, when removing an item from the agenda to explore, we typically remove it from the front of the agenda.
Some search techniques will add paths to the front of the agenda, treating it like a stack, while others will add to the back of the agenda, treating it like a queue. Some agendas are organized by heuristic value, others by path distance, and others by depth in the search tree. Your job will be to demonstrate your knowledge of search techniques by implementing different types of search and making slight modifications to how the agenda is accessed and updated.
Extending a Path
At a high level, you search for a path through a graph by starting with shorter paths then extending them into progressively longer paths until (ideally) you discover a path that terminates at the goal node. When we talk about extending a partial path, we mean that you consider every possible node that the path could reach next (i.e., all of the nodes that are neighbors of the last node in the path) and create a new, incrementally longer path for each possibility. Algorithmically, you'll collect those longer paths into a list then add them to the agenda in some order. During the search algorithm, you are continually taking paths from the agenda, in order to explore, and adding new extended paths back onto the agenda.
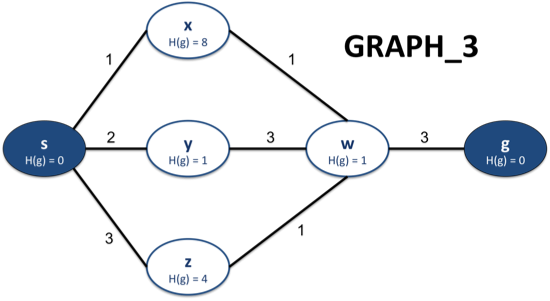
For example, in the following graph,
if your partial path is sxw, then the possible one-node extensions of sxw are sxwy, sxwz, and sxwg. Note that we exclude the possibility sxwx because we want our paths to be as short as possible, and so we always want to ignore any paths with loops.
Hint: When writing the function extensions(graph, path), you should ensure that the paths you create are new objects. If you try to extend a path by modifying (or "mutating") the existing path (for example, by using list .append() or .pop()) you may find yourself in a quagmire.
Note, for reference, all graphs can be found here.
An extended set makes optimal search more efficient
When you want to find not just any path, but the shortest path between two nodes, it is often useful to keep track of which nodes in the graph you've already extended (i.e., which nodes have been at the end of paths you've extended). We keep track of extended nodes so that we can take advantage of the following fact about paths:
- If the shortest route from the start to the goal passes through some intermediate node X, then the first part of that route must be shortest path between the start node and X.
Now consider how you can use this principle to avoid unnecessary searching when you use an algorithm, such as branch and bound, which is guaranteed to look at shorter paths before longer paths: If you extend a node X once, you know that you've found the shortest path from the start to X. Then if you later find a second path that ends in X, you can safely reject the second path; the second path takes longer to reach X than the first path, and so it cannot be part of the shortest, most direct path to the goal.
Algorithmically, you employ an extended set by maintaining a set or list of the nodes you've extended so far (i.e., nodes that have been at the end of paths you've extended). Then whenever you remove a path from the agenda, you can check the last node in the path and see if you've extended it already. If you have extended it already, you reject the path and continue with the next iteration of search. If you haven't extended it already, you can add the node to your extended set and proceed as usual.
When to Exit a Search
Non-optimal searches such as DFS, BFS, hill climbing and beam may exit either
- when it finds a path-to-goal in the agenda, or
- when a path-to-goal is first removed from the agenda.
Optimal searches such as branch & bound and A* must exit
- when a path-to-goal is first removed from the agenda.
Why is this the case? Because in an optimal search, the agenda is re-ordered by path length (or heuristic path length) at every iteration. Hence, a path-to-goal is not necessarily the best when it is added to the agenda; but, when it is removed from the agenda, it is guaranteed to have the shortest path length (or heuristic path length).
For the sake of consistency, in this lab, you should implement all your searches to exit
- when a path-to-goal is first removed from the agenda.
Types of Search
In this section, we will quickly go over the different types of search that we will ask you to code.
Each search algorithm should return an appropriate path from a given start node to a given goal node, or None if no such path is found. A path consists of a sequence of nodes, beginning with the start node and following edges in the graph to the goal node. The path should contain both the start and goal node.
In general, we never consider a path that reaches the same node twice (i.e., a path that contains a loop).
Blind Search
The first two types of search are "blind" searches.
In depth-first search (DFS), we extend paths from a given node, sorted lexicographically (e.g. the path ['S', 'A', 'Z'] comes before the path ['S', 'Z', 'A'], because SAZ comes before SZA in the English dictionary). New paths are added to the front of the agenda; in other words, the agenda is treated as a stack data structure. If backtracking is enabled, the algorithm will back up if it reaches a dead end and will continue to look for the goal node. In this lab, you should assume that your DFS allows backtracking and does not use an extended set.
Breadth-first search (BFS) is done similarly, except that new paths are added to the back of the agenda, thus simulating a queue data structure.
For a more detailed explanation of DFS and BFS, refer to Chapter 4 of the textbook (pages 4-6 of the pdf, pages 66-68 of the textbook).
Heuristic Search
You also will implement three types of heuristic search.
Hill Climbing
Hill climbing is very similar to depth-first search. There is only a slight modification to the ordering of paths that are added to the agenda. In particular, we always order the newly-added paths according to the best (smallest) heuristic distance from the current node to the goal node.
The hill-climbing procedure you define in this lab should use backtracking, for consistency with the other methods, even though hill climbing typically is not implemented with backtracking. Hill climbing is a fast, greedy algorithm, and it does not use an extended set.
For an explanation of hill climbing, refer to Chapter 4 of the textbook (pages 8-12 of the pdf, pages 70-74 of the textbook).
Best-First Search
Best-first search is similar to hill climbing in that it uses a heuristic, but best-first search always extends the "best" path in the agenda as determined by heuristic values to the goal. Like hill climbing and beam search, best-first search sorts paths by only the heuristic value, not the path length (as branch & bound does) or the path length + heuristic value (as A* does). Best-first search uses backtracking, but for this lab, it should not use an extended set.
For a brief explanation of best-first search, refer to Chapter 4 of the textbook (page 13 of the pdf, page 75 of the textbook).
Beam Search
Beam search is very similar to breadth-first search, but there is a modification for which paths are kept in the agenda. At any point in time, the agenda can only have up to w paths of a given length n (for all n), where n corresponds to the level or depth of the search graph; w is also known as the beam width. Beam search can be useful in situations where you want to reduce memory usage, especially when working with large graphs.
You will need to sort your paths by the graph's heuristic to ensure that only the best w paths at each level are in your agenda. You may want to use an array or dictionary to keep track of paths of different lengths. Beam search does NOT use an extended set, and does NOT use backtracking to the paths that are eliminated at each level.
Remember that w is the number of paths to keep at an entire level, not the number of paths to keep from each extended node.
For an explanation and an example of beam search, refer to Chapter 4 of the textbook (pages 13-14 of the pdf, pages 75-76 of the textbook). However, note that this example is incorrect according to how we do beam search: At the third level, the node B (with heuristic value 6.7, at the end of path S-D-E-B) should not be included: only C and F should be included, because the beam width is 2. Hence, at the fourth level, B should not be extended to A and C.
Optimal Search
The search techniques discussed so far have not taken into account the edge lengths in a graph. Instead, we were just trying to find one possible solution of many, perhaps with the aid of a heuristic. Optimal searches try to find the path with the shortest distance from the start node to the goal node. The search algorithms covered in this class that guarantee optimal solutions are:
- branch & bound
- A*, but only under certain conditions
Branch & Bound
Branch & bound is a modification of BFS. In particular, it takes into account the total path length so far. At every step, after adding the new paths to the agenda, it re-sorts the agenda by total combined path length so far, and explores the best (shortest) such path. We will ask you to implement this "basic" version of branch & bound which will not use an extended set.
For an explanation of branch & bound, refer to Chapter 5 of the textbook (starting at page 2 of the pdf, or page 82 of the textbook).
Branch & Bound: Variations
One also can add a heuristic to branch & bound, in which case one can consider the path with the least {heuristic estimate + path length} sum, and that is the path taken from the agenda to be explored.
In this lab, we ask you to implement two different branch & bound variations. The first will be using a heuristic with no extended set, and the second will be using an extended set, but no heuristic.
A*
A* is technically another variation of branch & bound, one that uses both a heuristic and an extended set. Note, however, that if the heuristic used is not consistent, then using an extended set can sometimes prevent A* from finding an optimal solution!
By the way, our definition of A* may differ slightly from others' definitions depending on who you ask, so don't be surprised if you see a different definition of A* in another class.
Problems
Part 1: Utility Functions
Your first task is to write four helper functions which may be useful in Parts 2 and 3:
def path_length(graph, path): def has_loops(path): def extensions(graph, path): def sort_by_heuristic(graph, goalNode, nodes):
A path is a list of nodes where each neighboring pair is connected by an edge in the graph. By convention, the start of the path is at index [0] and the end of the path is at index [-1].
path_length(graph, path) should return the length of a path, that is, the sum of the weights of the edges connecting the nodes. You may assume that the path is a valid sequence of edge-connected nodes in the graph, and that the path has at least one node in it. You may also assume that all edge-weights between these nodes are not None. If there is only one node in the path, your function should return 0.
has_loops(path) should return True if the path given contains a loop (i.e., reaches a node twice), otherwise False.
extensions(graph, path) should take a path and return a list of possible one-node extensions of that path, in lexicographic order. That is, your function should return a list of all possible paths that can be created by adding one more node to the given path (as described in Extending a Path, above), in lexicographic order.
sort_by_heuristic(graph, goalNode, nodes) should take a list of any nodes in the graph and sort them based on their heuristic value to the goalNode, from smallest to largest. The function should return the sorted list. (Hint: use sorted.) In case of a tie, sort nodes lexicographically.
Note that the API found at the end of this document will be helpful throughout the lab!
Part 2: Basic Search
In this lab, you will implement both depth-first and breadth-first search.
You may find Professor Winston's general search flowchart from lecture to be helpful. To jog your memory, we provide you rough pseudocode for a depth/breadth-first search:
1. Remove first path from agenda. If it ends with the goal node, return that path. 2. Otherwise, extend the path, and add all children to the agenda. 3. Repeat until there is nothing left in the agenda to be removed, in which case terminate with failure.
Take particular care in how you add children to the agenda. See our explanation of DFS and BFS above.
Your depth-first search should allow backtracking and should not use an extended set.
In the part of lab2.py labeled Part 2, implement basic_dfs(graph, startNode, goalNode) and basic_bfs(graph, startNode, goalNode), both of which take in an UndirectedGraph object, a start node, and a goal node, returning a path-to-goal if it exists, or None if such a path does not exist. Keep in mind that you may want to use the utility functions implemented in Part 1!
Part 3: Generic Search
You may have realized just how similar the DFS and BFS functions are: in fact, there is only a single key difference between the two. Indeed, the search methods we cover in 6.034 share many algorithmic similarities, and the implementations of each one may differ from others by only a single line of code. We want to explore these similarities (and differences) so that you can gain a conceptual understanding of how all of these search algorithms relate to each other, instead of feeling overwhelmed by so many different algorithms.
As such, we have created a generic search function generator which encapsulates all of the 6.034 search algorithms we have discussed.
Inputs for generic_search
generic_search has already been written for you. It takes in four arguments (which you will supply), two of which are functions themselves and two of which are boolean values. generic_search returns a function representing a particular search algorithm.
def generic_search(sort_new_paths_fn, add_paths_to_front_of_agenda, sort_agenda_fn, use_extended_set):
...
return search_algorithm
By defining appropriate values for the arguments, you can recreate any of the search algorithms we study in 6.034.
Below, we give an explanation of each of the four arguments to generic_search:
- sort_new_paths_fn(graph, goalNode, new_paths)
- When you extend a node, you create a list of new paths. Some algorithms will sort these paths before adding them to the agenda. The argument sort_new_paths_fn is a function of three arguments (the graph, the goal node, and the list of new paths) that performs the appropriate sorting routine; it returns the sorted list of new paths. If you don't want any sorting to happen, you can pass a function that simply returns the list of paths without changing it. The function do_nothing_fn, provided for you, accomplishes this.
- add_paths_to_front_of_agenda
- Some algorithms will add new paths to the front of the agenda (like a stack). Others will add new paths to the back of the agenda (like a queue). When the argument add_paths_to_front_of_agenda is True, paths will get added to the front of the agenda. Otherwise, paths will get added to the back.
- sort_agenda_fn(graph, goalNode, agenda_paths)
- After new paths are added to the agenda, some algorithms will then sort the entire agenda. The argument sort_agenda_fn is a function of three arguments (the graph, the goal node, and agenda) that performs the appropriate sorting routine; it returns a sorted agenda. If you don't want any sorting to happen, you can pass a function that simply returns the list of paths without changing them (do_nothing_fn). Note that if you do sort the agenda, then the previous two arguments become irrelevant (it no longer matters whether you added new paths to the front, or whether you sorted them before adding them to the agenda).
- use_extended_set
- Some algorithms use an extended set. Set use_extended_set to True to maintain an extended set, else set it to False.
Examples for using generic_search
To create a search algorithm that does not sort new paths, adds paths to the front of the agenda, does not sort the agenda, and does not use an extended set, you can call generic_search like this:
my_search_fn = generic_search(do_nothing_fn, True, do_nothing_fn, False)
You can then call your search algorithm on a graph:
my_path = my_search_fn(graph, startNode, goalNode)
You can also call generic_search directly on a list of arguments (such as generic_dfs) like this:
path = generic_search(*generic_dfs)(graph, startNode, goalNode)
If you want to test your search algorithm on a provided graph, you can use one of the graphs shown in Graphs for Testing. For example:
path = generic_search(*generic_dfs)(graph1, 'S', 'G')
Your Task
Please implement the following search algorithms by designing the correct arguments to pass to the generic search algorithm. Your answer to each should be an ordered list of the appropriate four arguments to generic_search. No argument should be None. Note that the definitions of these search functions should correspond to the explanations of the search algorithms given in Types of Search.
generic_dfs = [None, None, None, None] generic_bfs = [None, None, None, None] generic_hill_climbing = [None, None, None, None] generic_best_first = [None, None, None, None] generic_branch_and_bound = [None, None, None, None] generic_branch_and_bound_with_heuristic = [None, None, None, None] generic_branch_and_bound_with_extended_set = [None, None, None, None] generic_a_star = [None, None, None, None]
For this, you will need to write your own path-sorting functions. Each sorting function should take in a graph, a goal node, and list of paths, and then return a list of paths. For example: sorted_paths = my_sorting_fn(graph, goalNode, paths). We recommend that you avoid modifying the original list of paths in your sorting function.
Break ties lexicographically. For your convenience, here is a tie-breaking function that you can add to lab2.py to use in your sorting, extensions, and sort_by_heuristic functions:
def break_ties(paths):
return sorted(paths)
Optional: Generic Beam Search
Beam search is trickier to implement with generic_search, so it's optional. If you want to run local tests to test your generic_beam, change the boolean TEST_GENERIC_BEAM to True in lab2.py. There are no online tests for generic_beam.
To implement generic_beam, fill in the four arguments:
generic_beam = [None, None, None, None]
The sort_agenda_fn for beam search takes a fourth argument, beam_width. For example:
sorted_beam_agenda = my_beam_sorting_fn(graph, goalNode, paths, beam_width)
Similarly, the search algorithm produced by generic_search for beam search will take an additional argument, beam_width. For example:
my_beam_fn = generic_search(*generic_beam)
my_beam_path = my_beam_fn(graph, startNode, goalNode, beam_width)
Hint: You can implement beam search in a way almost identical to BFS. The main difference is that beam search will need to limit the number of paths whenever an entire level has been expanded. You can do this by defining a sort_agenda_fn function that checks whether an entire level has been extended. If it has, the function should limit the number of paths in the agenda. If it hasn't, the function should do nothing to the agenda.
Part 4: Heuristics
Admissibility and Consistency
A heuristic value gives an approximation from a node to a goal. You've learned that in order for the heuristic to be admissible, the heuristic value for every node in a graph must be less than or equal to the distance of the 'shortest path from the goal to that node (Hint: have you implemented any search algorithms in Part 3 that are guaranteed to return the shortest path?). In order for a heuristic to be consistent, for each edge in the graph, the edge length must be greater than or equal to the absolute value of the difference between the two heuristic values of its nodes.
For this part, complete the following functions, which return True iff the heuristics for the given goal node are admissible or consistent, respectively, and False otherwise:
def is_admissible(graph, goalNode): def is_consistent(graph, goalNode):
Hint: For is_consistent, it's sufficient to check only neighboring nodes, rather than checking all pairs of nodes in the graph.
Optional: Picking Heuristics
- Warning!
- You must complete generic_a_star (and pass all related tests) before starting this section. Some of the tests in this section will use your A* algorithm.
This optional section is intended to help you test your understanding of heuristics. To check your heuristics, you can run local tests by changing the boolean TEST_HEURISTICS to True. There are no online tests for this section.
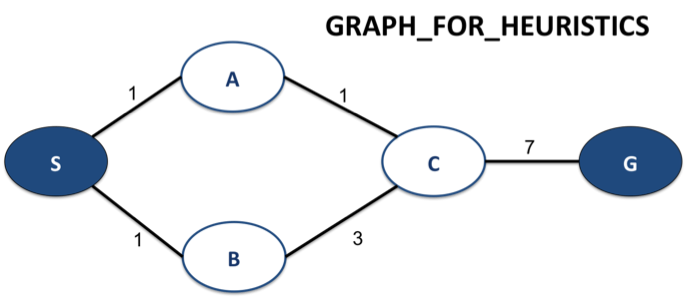
The questions in this section use the following graph:
For heuristic_1, pick heuristic values so that, for the goal node G, the heuristic is both admissible and consistent. Fill in the values by replacing the list of five None's with five numbers:
[h1_S, h1_A, h1_B, h1_C, h1_G] = [None, None, None, None, None]
For heuristic_2, pick heuristic values so that, for the goal node G, the heuristic is admissible but NOT consistent.
For heuristic_3, pick heuristic values so that, for the goal node G, the heuristic is admissible but A* returns a non-optimal (i.e., not the shortest) path to the goal. That is, it should return the non-optimal path (S-B-C-G).
For heuristic_4, pick heuristic values so that, for the goal node G, the heuristic is admissible but NOT consistent, yet A* still finds the optimal (shortest) path to the goal, i.e., (S-A-C-G).
Part 5: Multiple Choice
Fill in the answer to each question in ANSWER_i at the bottom of lab2.py. Each answer should be a string: '1', '2', '3', or '4'.
Question 1: You are in a new house and want to know where all the bedrooms are. You want to find the bedrooms as quickly as possible. Which algorithm should you use?
1. Breadth First Search
2. British Museum
3. A*
4. Branch and Bound with Extended Set
Question 2: You are playing a game in which you are in a maze, and you are trying to exit. All the rooms are different colors, so you know which ones you've been in before, but there is no way of telling where you are in the maze with respect to the exit (until you reach the exit). You win the game if you exit the maze as quickly as possible. Which algorithm should you use?
1. Breadth First Search
2. British Museum
3. A*
4. Branch and Bound with Extended Set
Question 3: Your friend Hammer is an amateur map-maker, and you have asked for directions for a route from your hometown of Oakvale to Bowerstone Marketplace. Your goal is to reach as few towns as possible along the way. Hammer is very bad at estimating distances and remembering where she's already been, so she wants to use the simplest algorithm possible to find what path you should take. Which algorithm should Hammer use?
1. Breadth First Search
2. British Museum
3. A*
4. Branch and Bound with Extended Set
Question 4: Hammer goes to map-maker school and becomes better at distances and memory. Now you ask her for directions for the shortest distance from Bowerstone Marketplace to Silverpine. Which algorithm should Hammer use?
1. Breadth First Search
2. British Museum
3. A*
4. Branch and Bound with Extended Set
API: Graphs and Edges
The file search.py contains definitions for graphs and edges. The relevant information is described here, so you shouldn't need to read the file.
UndirectedGraph
A graph is an object of type UndirectedGraph.
An UndirectedGraph object has the following attributes (fields):
- nodes
- A list of all nodes in the graph.
- edges
- A list of all edges in the graph.
An UndirectedGraph object has the following class methods:
- get_neighbors(node1)
- Given a node node1, returns a list of all nodes that are directly connected to node1
- get_neighboring_edges(node1)
- Given a node node1, returns a list of all edges that have node1 as their startNode.
- get_edge(node1, node2)
- Given two nodes, returns the edge that directly connects them (or None if there is no such edge).
- is_neighbor(node1, node2)
- Given two nodes, returns True if there is an edge that connects them, or False if there is no such edge.
- get_heuristic_value(node1, goalNode)
- Given two nodes node1 and goalNode, returns the heuristic estimate of the distance from node1 to goalNode.
- copy()
- Returns a (deep) copy of the graph.
Edge
An edge is an object of type Edge. An Edge object has the following attributes:
- startNode
- The start node of this edge.
- endNode
- The end node of this edge.
- length
- A positive number describing the edge's length, or None if the edge has no length specified or if it is irrelevant.
You can also copy an Edge by using the .copy() method, which returns a deep copy of the edge.
You can check whether two edges e1 and e2 are the same with e1 == e2.
Lastly, you should note that we do not have a dedicated class for nodes (vertices). Nodes are represented as strings or integers.
Resource: Graphs for Testing
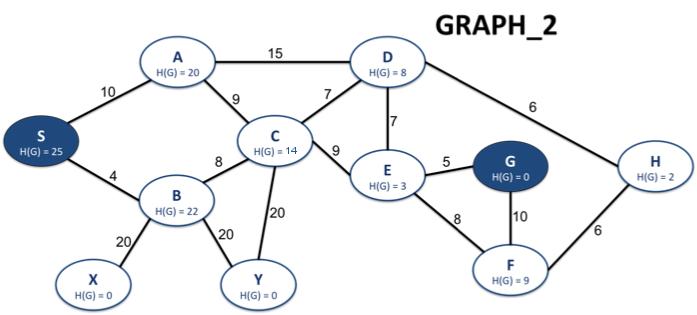
Here are some sample graphs that are used in the tester and which you can use to test and debug your functions. The graphs have been imported into lab2.py by their names. In other words, if you want to access (say) GRAPH_2, it's stored in the variable GRAPH_2.
The graphs come from the files graphs.txt and read_graphs.py, which you should not need to read.
Survey
Please answer these questions at the bottom of your lab file:
- NAME: What is your name? (string)
- COLLABORATORS: Other than 6.034 staff, whom did you work with on this lab? (string, or empty string if you worked alone)
- HOW_MANY_HOURS_THIS_LAB_TOOK: Approximately how many hours did you spend on this lab? (number or string)
- WHAT_I_FOUND_INTERESTING: Which parts of this lab, if any, did you find interesting? (string)
- WHAT_I_FOUND_BORING: Which parts of this lab, if any, did you find boring or tedious? (string)
- (optional) SUGGESTIONS: What specific changes would you recommend, if any, to improve this lab for future years? (string)
(We'd ask which parts you find confusing, but if you're confused you should really ask a TA.)
When you're done, run the online tester to submit your code.
FAQ
Q: How should A* behave if given a bad (inadmissible or inconsistent) heuristic?
A: The A* algorithm should still search for and return a path; however, the path returned is not guaranteed to be optimal. In practice, you can patch A* so that it will return the shortest path even if the heuristic is bad (see Chapter 5 of the textbook) --- but for this lab, we ask you to implement naive A*, which optimistically assumes that the first path it finds to each node is the shortest.
Q: How should I break ties if two paths have the same length?
A: See tie-breaking, above: Break ties lexicographically. (For example, the path ['S', 'A', 'Z'] comes before the path ['S', 'Z', 'A'], because SAZ would come before SZA in the English dictionary.)