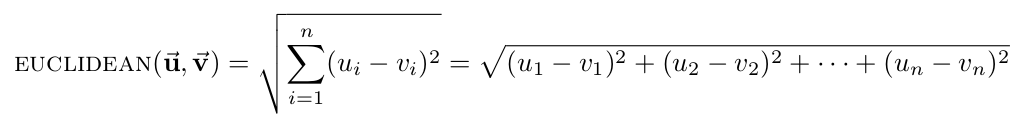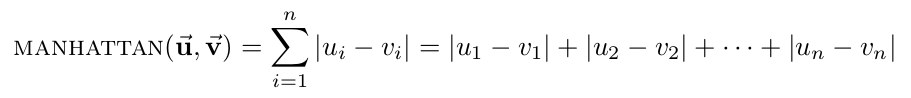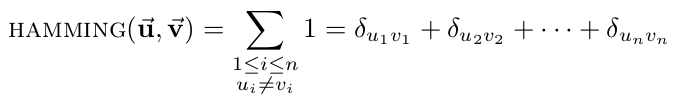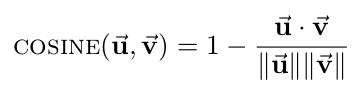Lab 6: k-Nearest Neighbors

From 6.034 Wiki

(Difference between revisions)

Current revision

You are expected, but not required, to complete this portion of the lab by 10:00pm Tuesday, October 20. The official, final deadline for both Part 1 and Part 2 is 10:00pm Thursday, October 29.

k-Nearest Neighbors is a simple yet popular method for classifying data points. Per its name, it works by looking for training points near a given test point, where "near" is defined by some sort of metric. In particular, the classifier finds the k nearest training points to the test point, and counts up how many of each neighbor corresponds to a certain classification: the classification with the most nearby points is the one applied to the test point.

Part 2A: Drawing boundaries

Before we start coding, let's warm up by reviewing decision boundaries. We will be considering decision boundaries for ID trees as well as for kNN (with k = 1).

Below are sketches of 4 different data sets in Cartesian space, with numerous ways of drawing decision boundaries for each. For each sketch, answer the following question by filling in BOUNDARY_ANS_n (for n from 1 to 14) with an int 1, 2, 3, or 4:

Which method could create the decision boundaries drawn in the sketch? Greedy, disorder-minimizing ID tree, using only tests of the form "X > threshold" or "Y > threshold" 1-nearest neighbors using Euclidean distance Both Neither

For explanations of the answers to some of these questions, search for "#BOUNDARY_ANS_n" in tests.py, for the appropriate value of n.

Part 2B: Distance metrics

When doing k-nearest neighbors, we aren't just restricted to straight-line (Euclidean) distance to compute how far away two points are from each other. We can use many different distance metrics. In 6.034, we cover four such metrics:

Euclidean distance: the straight-line distance between two points.

Manhattan distance: the distance between two points assuming you can only move parallel to axes. In two dimensions, you can conceptualize this as only being able to move along the "grid lines."

Hamming distance: the number of differing corresponding components between two vectors.

Cosine distance: compares the angle between two vectors, where each point is represented as a vector from the origin to the point's coordinates. Note that cosine is a similarity measure, not a difference measure, because cos(0)=1 means two vectors are "perfectly similar," cos(90 deg)=0 represents two "perfectly orthogonal" vectors, and cos(180 deg)=-1 corresponds to two "maximally dissimilar" (or "perfectly opposite") vectors. For our code, however, we need this metric to be a difference measure so that smaller distances means two vectors are "more similar," to match all of the other distance metrics. Accordingly, we will define the cosine distance to be 1 minus the cosine of the angle between two vectors, so that our cosine distance varies between 0 (perfectly similar) and 2 (maximally dissimilar). Thus, the formula for cosine distance is:

It's also possible to transform data instead of using a different metric -- for instance, transforming to polar coordinates -- but in this lab we will only work with distance metrics in Cartesian coordinates.

We'll start with some basic functions for manipulating vectors, which may be useful for cosine_distance. For these, we will represent an n-dimensional vector as a list or tuple of n coordinates. dot_product should compute the dot product of two vectors, while norm computes the length of a vector. (There is a simple implementation of norm that uses dot_product.) Implement both functions:

def dot_product(u, v):

def norm(v):

Next, you'll implement each of the four distance metrics. For the rest of the k-nearest neighbors portion of this lab, we will represent data points as Point objects (described below in the API). Because Point objects are iterable (e.g. you can do for coord in point:), you should be able to call your vector methods on them directly. Each distance function should take in two Points and return the distance between them as a float or int. Python hint: The built-in Python keyword zip may be useful. To learn more, type help(zip) in a Python command line, or read about it online.

Implement each distance function:

def euclidean_distance(point1, point2):

def manhattan_distance(point1, point2):

def hamming_distance(point1, point2):

def cosine_distance(point1, point2):

Part 2C: Classifying Points

Now that we have defined four distance metrics, we will use them to classify points using k-nearest neighbors with various values of k.

First, write a function get_k_closest_points that takes in a point (a Point object), some data (a list of Point objects), a number k, and a distance metric (a function, such as euclidean_distance), and returns the k points in the data that are nearest to the input point, according to the distance metric. In case of a tie, sort by point.coords (i.e. break ties lexicographically by coordinates). This function can be written cleanly in about five lines.

def get_k_closest_points(point, data, k, distance_metric):

A note about ties: There are two ways to get ties when classifying points using k-nearest neighbors.

If two or more training points are equidistant to the test point, the "k nearest" points may be undefined. If the equidistant points have the same classification, it doesn't make a difference, but in some cases they could cause the classification to be ambiguous. In this lab, these cases are handled in get_k_closest_points by breaking ties lexicographically.
If the two most likely classifications are equally represented among the k nearest training points, the classification is ambiguous. In other words, the k-nearest neighbors are voting on a classification, and if the vote is tied, there needs to be some mechanism for breaking the tie. In this lab, we will assume that there are no voting ties, so you don't need to worry about tie-breaking. (All of the test cases in this section are designed to ensure that there will not be any voting ties.)

Your task is to use that to write a function that classifies a point, given a set of data (as a list of Points), a value of k, and a distance metric (a function):

def knn_classify_point(point, data, k, distance_metric):

Python hint: To get the mode of a list, there's a neat one-line trick using max with the key argument, the list.count function, and converting a list to a set to get the unique elements. .count is a built-in list method that counts how many times an item occurs in a list. For example, [10, 20, 20, 30].count(20) -> 2.

Part 2D: Choosing the best k and distance metric via cross-validation

There are many possible implementations of cross validation, but the general idea is to separate your data into a training set and a test set, then use the test set to determine how well the training parameters worked. For k-nearest neighbors, this means choosing a value of k and a distance metric, then testing each point in the test set to see whether they are classified correctly. The "cross" part of cross-validation comes from the idea that you can re-separate your data multiple times, so that different subsets of the data take turns being in the training and test sets, respectively.

For the next function, you'll implement a specific type of cross-validation known as leave-one-out cross-validation. If there are n points in the data set, you'll separate the data n times into a training set of size n-1 (all the points except one) and a test set of size one (the one point being left out). Implement the function cross_validate, which takes in a set of data, a value of k, and a distance metric, and returns the fraction of points that were classified correctly using leave-one-out cross-validation.

def cross_validate(data, k, distance_metric):

Use your cross-validation method to write a function that takes in some data (a list of Points) and tries every combination of reasonable values of k and the four distance metrics we defined above, then returns a tuple (k, distance_metric) representing the value of k and the distance metric that produce the best results with cross validation:

def find_best_k_and_metric(data):

Part 2E: More Multiple Choice

Questions 1-3: More tree classification

These questions refer to the k-nearest neighbors data on classifying trees, from 2014 Quiz 2, Part B.

Recall the following terms:

Overfitting: Occurs when small amounts of noise in the training data are treated as meaningful trends in the population. (i.e. when relying too heavily on the data, or overutilizing the data, causes a poor classification rate)
Underfitting: Occurs when the algorithm blurs out differences in the training data that reflect genuine trends in the population. (i.e. when ignoring information in the data, or underutilizing the data, causes a poor classification rate)

kNN Question 1: Consider the results of cross-validation using k=1 and the Euclidean distance metric. Why is 1 not a good value for k? Answer "Overfitting" or "Underfitting" in kNN_ANSWER_1.

kNN Question 2: Consider the results of cross-validation using k=7 and the Euclidean distance metric. Why is 7 not a good value for k? Answer "Overfitting" or "Underfitting" in kNN_ANSWER_2.

kNN Question 3: Euclidean distance doesn't seem to do very well with any value of k (for this data). Which distance metric yields the highest classification rate for this dataset? Answer 1, 2, 3, or 4 in kNN_ANSWER_3:

Euclidean distance
Manhattan distance
Hamming distance
Cosine distance

Questions 4-7: Choosing metrics

kNN Question 4: Suppose you wanted to classify a mysterious drink as coffee, energy drink, or soda based on the amount of caffeine and amount of sugar per 1-cup serving. Coffee typically contains a large amount of caffeine, lemonade typically contains a large amount of sugar, and energy drinks typically contain a large amount of both. Which distance metric would work best, and why? Answer 1, 2, 3, or 4 in kNN_ANSWER_4:

Euclidean distance, because you're comparing standard numeric quantities
Manhattan distance, because it makes sense to array the training data points in a grid
Hamming distance, because the features "contains caffeine" and "contains sugar" are boolean values
Cosine distance, because you care more about the ratio of caffeine to sugar than the actual amount

kNN Question 5: Suppose you add a fourth possible classification, water, which contains no caffeine or sugar. Now which distance metric would work best, and why? Answer 1, 2, 3, or 4 in kNN_ANSWER_5:

Euclidean distance, because you're still comparing standard numeric quantities, and it's now more difficult to compare ratios
Manhattan distance, because there are now four points, so it makes even more sense to array them in a grid
Hamming distance, because the features "contains caffeine" and "contains sugar" are still boolean values
Cosine distance, because you still care more about the ratio of caffeine to sugar than the actual amount

kNN Question 6: While visiting Manhattan, you discover that there are 3 different types of taxis, each of which has a distinctive logo. Each type of taxi comes in many makes and models of cars. Which distance metric would work best for classifying additional taxis based on their logos, makes, and models? Answer 1, 2, 3, or 4 in kNN_ANSWER_6:

Euclidean distance, because there's a lot of variability in make and model
Manhattan distance, because the streets meet at right angles (and because you're in Manhattan and classifying taxicabs)
Hamming distance, because the features are non-numeric
Cosine distance, because it will separate taxis by how different their makes and models are

kNN Question 7: Why might an ID tree work better for classifying the taxis from Question 6? Answer 1, 2, 3, or 4 in kNN_ANSWER_7:

k-nearest neighbors requires data to be graphed on a coordinate system, but the training data isn't quantitative
Some taxis may have the same make and model, and k-nearest neighbors can't handle identical training points
An ID tree can ignore irrelevant features, such as make and model
Taxis aren't guaranteed to stay within their neighborhood in Manhattan

For explanations of the answers to some of these questions, search for "#kNN_ANSWER_n" in tests.py, for the appropriate value of n.

Point API

The Point class supports iteration (to iterate through the coordinates).

A Point has the following attributes:

name: The name of the point (a string), if defined.

coords: The coordinates of the point, represented as a vector (a tuple or list of numbers).

classification: The classification of the point, if known.

Lab 6: k-Nearest Neighbors

From 6.034 Wiki

Current revision

Contents

Part 2A: Drawing boundaries

Part 2B: Distance metrics

Part 2C: Classifying Points

Part 2D: Choosing the best k and distance metric via cross-validation

Part 2E: More Multiple Choice

Questions 1-3: More tree classification

Questions 4-7: Choosing metrics

Point API

Views

Personal tools

Navigation

Search

Toolbox

@@ Line 1: / Line 1: @@
-== ID Trees and k-Nearest Neighbors ==
+You are expected, but not required, to complete this portion of the lab by '''10:00pm Tuesday, October 20'''.
+The official, final deadline for both Part 1 and Part 2 is '''10:00pm Thursday, October 29'''.
-This lab covers both ID trees (classification trees) and k-nearest neighbors. It is a long lab, so we do suggest you start working on it sooner rather than later.
-Although we learn about k-nearest neighbors before classification trees, this lab tackles the two topics in reverse order. This is primarily because the topic of ID trees more comfortably bridges the gap between rule-based artificial intelligence and computation-based machine learning methods.
+k-Nearest Neighbors is a simple yet popular method for classifying data points. Per its name, it works by looking for training points near a given test point, where "near" is defined by some sort of metric. In particular, the classifier finds the ''k'' nearest training points to the test point, and counts up how many of each neighbor corresponds to a certain classification: the classification with the most nearby points is the one applied to the test point.
-You are, of course, free to do the problems in whatever order you wish.
+== Part 2A: Drawing boundaries ==
-As always, we strongly recommend reading the [[#API_Reference_Documentation | API section]] before writing any code. Otherwise, you may find yourself re-writing code that needn't be written again.
+Before we start coding, let's warm up by reviewing decision boundaries. We will be considering decision boundaries for ID trees as well as for kNN (with ''k'' = 1).
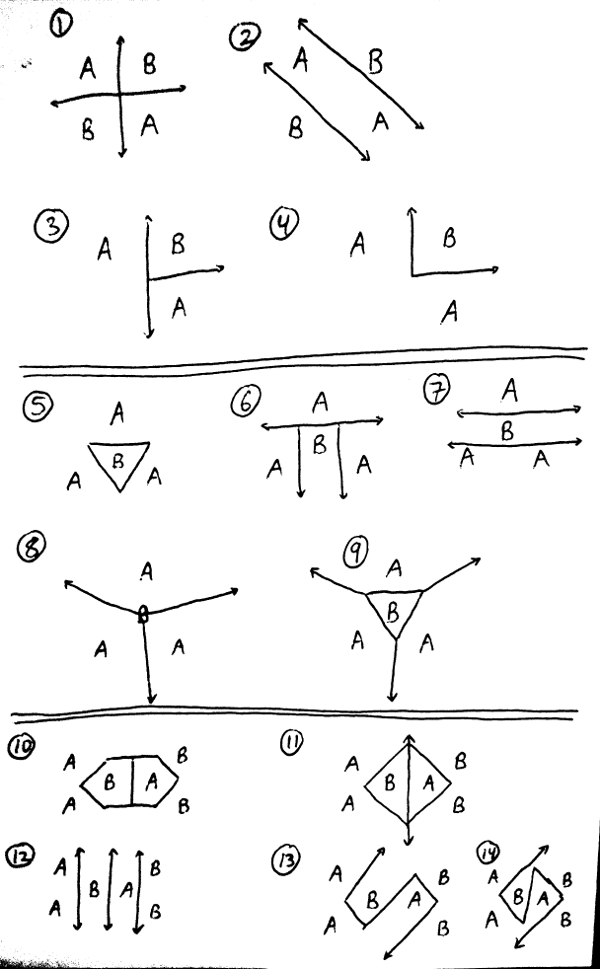
+Below are sketches of 4 different data sets in Cartesian space, with numerous ways of drawing decision boundaries for each. For each sketch, answer the following question by filling in BOUNDARY_ANS_n (for n from 1 to 14) with an int 1, 2, 3, or 4:
-== Identification Trees ==
+;Which method could create the decision boundaries drawn in the sketch?
+:#Greedy, disorder-minimizing ID tree, using only tests of the form "X > threshold" or "Y > threshold"
+:#1-nearest neighbors using Euclidean distance
+:#Both
+:#Neither
-In this section of the lab, we will first warm up by using an ID tree to classify points. Then, we will learn how to construct new ID trees from raw data, using the techniques we learned in class.
+[[Image:Lab5_decision_boundary_images.jpg]]
-=== Part 1A: Using an ID Tree to classify unknown points ===
+For explanations of the answers to some of these questions, search for "#BOUNDARY_ANS_n" in tests.py, for the appropriate value of n.
-In this section, we will represent an ID tree recursively as a tree of [[#IdentificationTreeNode | <tt>IdentificationTreeNode</tt> objects]].
+== Part 2B: Distance metrics ==
-We will represent a data point as a dictionary mapping attributes to values.  For example, the following could represent a data point in our vampires example from lecture:
+When doing k-nearest neighbors, we aren't just restricted to straight-line (Euclidean) distance to compute how far away two points are from each other. We can use many different distance metrics. In 6.034, we cover four such metrics:
- datapoint1 = {"name":"person1", "Vampire?":"Vampire", "Shadow":"?", "Eats Garlic":"No", "Complexion":"Ruddy", "Accent":"Odd"}
+* '''Euclidean distance''': the straight-line distance between two points.
+[[Image:Euclidean distance.png|center]]
+* '''Manhattan distance''': the distance between two points assuming you can only move parallel to axes. In two dimensions, you can conceptualize this as only being able to move along the "grid lines."
+[[Image:Manhattan distance.png|center]]
+* '''Hamming distance''': the number of differing corresponding components between two vectors.
+[[Image:Hamming distance.png|center]]
+* '''Cosine distance''': compares the angle between two vectors, where each point is represented as a vector from the origin to the point's coordinates.  Note that cosine is a similarity measure, not a difference measure, because cos(0)=1 means two vectors are "perfectly similar," cos(90 deg)=0 represents two "perfectly orthogonal" vectors, and cos(180 deg)=-1 corresponds to two "maximally dissimilar" (or "perfectly opposite") vectors.  For our code, however, we need this metric to be a difference measure so that smaller distances means two vectors are "more similar," to match all of the other distance metrics.  Accordingly, we will define the cosine distance to be 1 minus the cosine of the angle between two vectors, so that our cosine distance varies between 0 (perfectly similar) and 2 (maximally dissimilar).  Thus, the formula for cosine distance is:
+[[Image:Cosine distance.png|center]]
-To begin, let's use an ID tree to classify a point! Classifying a point using an ID tree is straight-forward. We recursively apply the current node's classifier to the data point, using the result to choose which branch to take to the child node. If a "leaf" node is ever encountered, that node gives the final classification of the point.
+It's also possible to transform data instead of using a different metric -- for instance, transforming to polar coordinates -- but in this lab we will only work with distance metrics in Cartesian coordinates.
-Write a function <tt>id_tree_classify_point</tt> that takes in a point (represented as a dictionary) and an ID tree (represented as a <tt>IdentificationTreeNode</tt>) and uses the ID tree to classify the point (even if the point already has a classification defined), returning the final classification.
+We'll start with some basic functions for manipulating vectors, which may be useful for <tt>cosine_distance</tt>. For these, we will represent an ''n''-dimensional vector as a list or tuple of ''n'' coordinates.
+<tt>dot_product</tt> should compute the dot product of two vectors, while <tt>norm</tt> computes the length of a vector.  (There is a simple implementation of <tt>norm</tt> that uses <tt>dot_product</tt>.)  Implement both functions:
-  def id_tree_classify_point(point, id_tree):
+  def dot_product(u, v):
-(Note carefully that the <tt>point</tt> argument in this function and in all ID-tree questions in this lab has nothing to do with the [[#Point_.28for_kNN.29 | Point API]] introduced later on in the kNN section of the lab!)
+ def norm(v):
-This function can be written cleanly in 3-4 lines, either iteratively or recursively. If you're not sure how, check out the available methods in the [[#IdentificationTreeNode | <tt>IdentificationTreeNode</tt> API]].
-=== Part 1B: Splitting Data with a Classifier ===
+Next, you'll implement each of the four distance metrics.  For the rest of the k-nearest neighbors portion of this lab, we will represent data points as [[#Point_(for_kNN)|Point]] objects (described below in the API).  Because Point objects are iterable (e.g. you can do <tt>for coord in point:</tt>), you should be able to call your vector methods on them directly.  Each distance function should take in two Points and return the distance between them as a float or int. ''Python hint'': The built-in Python keyword <tt>zip</tt> may be useful.  To learn more, type <tt>help(zip)</tt> in a Python command line, or read about it online.
-In order to actually construct an ID tree, we'll need to work directly with ''classifiers'', also known as ''tests''. Recall that at each node of an ID tree, unless the training data at the node is homogeneous, we pick the best available classifier to split the data up. This same logic is repeated at every level of the tree, with each node taking as training data the data points sorted into that category by the node above it.
+Implement each distance function:
-We will represent each classifier as a [[#Classifier | <tt>Classifier</tt> object]].
+ def euclidean_distance(point1, point2):
-Implement <tt>split_on_classifier</tt>, which should take in a list of points and a particular <tt>Classifier</tt>, returning a dictionary mapping each possible feature value for that classifier to a list of the points that have that value (i.e. the data in its branch):
+ def manhattan_distance(point1, point2):
-  def split_on_classifier(data, classifier):
+  def hamming_distance(point1, point2):
-For example, <tt>split_on_classifier(angel_data, feature_test("Shape"))</tt> should return a dictionary mapping "Human" to a list of four points and "Animal" to a list of two points.
+ def cosine_distance(point1, point2):
-=== Part 1C: Calculating Disorder ===
+== Part 2C: Classifying Points ==
-One of the first steps in constructing an ID tree is to calculate disorder.  We'll start by coding the information-disorder equations to calculate the disorder of a branch or test.
+Now that we have defined four distance metrics, we will use them to classify points using k-nearest neighbors with various values of k.
-However, before we start, we will review some nomenclature:
+First, write a function <tt>get_k_closest_points</tt> that takes in a point (a Point object), some data (a list of Point objects), a number k, and a distance metric (a function, such as euclidean_distance), and returns the k points in the data that are nearest to the input point, according to the distance metric. In case of a tie, sort by <tt>point.coords</tt> (i.e. break ties lexicographically by coordinates). This function can be written cleanly in about five lines.
-* A '''branch''', conceptually, is a set of data representing the points that, upon applying a particular classifier (e.g. "Eats garlic") to a set of many points, all result in the same feature result. For example, suppose our data set is <tt>[p1, p2, p3, p4, p5, p6]</tt>, where each of <tt>p1, ...</tt> are Python dictionaries representing data points. Then, for example, applying the "Eats garlic" classifier to the data could yield two branches, one for all of the points with <tt>"Eats garlic": "Yes"</tt> and one for all of the points with <tt>"Eats garlic": "No"</tt>.
-* A '''test''' (also known as a '''decision stump''' or '''feature test''', and sometimes referred to loosely as a '''classifier''') encompasses all of the ''branches'' for a particular classifier. In the example for branches above, the two branches ("Yes" and "No") together constitute the decision stump for the "Eats garlic" classifier, often referred to concisely as the ''test''.
-Now, recall that the information disorder of a branch represents how different the values are in that branch. A branch whose points all have the same final classification is ''homogeneous'', and has a disorder of 0. On the other hand, a branch with many different values has a very high disorder. For example, a branch that has two points with classification <tt>"Vampire"</tt> and two points with classification <tt>"Not Vampire"</tt> has a disorder of 1.
+ def get_k_closest_points(point, data, k, distance_metric):
-The formula we use for disorder originates in information theory, and is described in detail on page 429 of [http://courses.csail.mit.edu/6.034f/ai3/ch21.pdf the reading].
+'''A note about ties:''' There are two ways to get ties when classifying points using k-nearest neighbors.
+#If two or more training points are equidistant to the test point, the "k nearest" points may be undefined.  If the equidistant points have the same classification, it doesn't make a difference, but in some cases they could cause the classification to be ambiguous.  In this lab, these cases are handled in <tt>get_k_closest_points</tt> by breaking ties lexicographically.
+#If the two most likely classifications are equally represented among the k nearest training points, the classification is ambiguous.  In other words, the k-nearest neighbors are voting on a classification, and if the vote is tied, there needs to be some mechanism for breaking the tie.  In this lab, we will assume that there are no voting ties, so you don't need to worry about tie-breaking.  (All of the test cases in this section are designed to ensure that there will not be any voting ties.)
-As a quick example, suppose we have a data set representing different types of balls:
+Your task is to use that to write a function that classifies a point, given a set of data (as a list of Points), a value of k, and a distance metric (a function):
-<pre>
+ def knn_classify_point(point, data, k, distance_metric):
-ball1 = {"size": "big", "color": "brown", "type": "basketball"}
-ball2 = {"size": "big", "color": "white", "type": "soccer"}
-ball3 = {"size": "small", "color": "white", "type": "lacrosse"}
-ball4 = {"size": "small", "color": "blue", "type": "lacrosse"}
-ball5 = {"size": "small", "color": "yellow", "type": "tennis"}
-ball_data = [ball1, ball2, ball3, ball4, ball5]
-</pre>
-Then, applying the classifier for "size" yields two branches:
- branch1 = [ball1, ball2]
+''Python hint'': To get the mode of a list, there's a neat one-line trick using <tt>max</tt> with the <tt>key</tt> argument, the <tt>list.count</tt> function, and converting a list to a set to get the unique elements. <!--max(set(my_list), key=my_list.count)--> <tt>.count</tt> is a built-in list method that counts how many times an item occurs in a list.  For example, <tt>[10, 20, 20, 30].count(20)</tt> -> <tt>2</tt>.
-  branch2 = [ball3, ball4, ball5]
+<!--* <tt>list.count</tt>: <tt>.count</tt> is a built-in list method that counts how many times an item occurs in a list.  For example, <tt>[10, 20, 20, 30].count(20)</tt> -> <tt>2</tt>.
+* <tt>set</tt>: Recall from Lab 0 that a set is handy way to count or enumerate the unique items in a list.
+-->
-where <tt>branch1</tt> represents balls that are big and <tt>branch2</tt> represents balls that are small. The disorder of <tt>branch1</tt> is 1, because the classifications in this branch are <tt>["basketball", "soccer"]</tt>. However, the disorder of <tt>branch2</tt> is roughly 0.9, because the classifications in this branch are <tt>["lacrosse", "lacrosse", "tennis"]</tt>.
+== Part 2D: Choosing the best k and distance metric via cross-validation ==
-However, applying the classifier for "color" instead yields
+There are many possible implementations of cross validation, but the general idea is to separate your data into a training set and a test set, then use the test set to determine how well the training parameters worked.  For k-nearest neighbors, this means choosing a value of k and a distance metric, then testing each point in the test set to see whether they are classified correctly.  The "cross" part of cross-validation comes from the idea that you can re-separate your data multiple times, so that different subsets of the data take turns being in the training and test sets, respectively.
-  branch1 = [ball1]
+For the next function, you'll implement a specific type of cross-validation known as leave-one-out cross-validation.  If there are n points in the data set, you'll separate the data n times into a training set of size n-1 (all the points except one) and a test set of size one (the one point being left out).  Implement the function <tt>cross_validate</tt>, which takes in a set of data, a value of k, and a distance metric, and returns the fraction of points that were classified correctly using leave-one-out cross-validation.
- branch2 = [ball2, ball3]
-  branch3 = [ball4]
- branch4 = [ball5]
-Here, the disorders of <tt>branch1</tt>, <tt>branch3</tt>, and <tt>branch4</tt> are all 0, and the disorder of <tt>branch2</tt> is 1.
+ def cross_validate(data, k, distance_metric):
-Now, complete the function <tt>branch_disorder</tt>. <tt>branch_disorder</tt> should take in a list of data points ''in the current branch'' as well as the classifier for determining the final classification of the points, and return the disorder of the branch, as a number:
+Use your cross-validation method to write a function that takes in some data (a list of Points) and tries every combination of reasonable values of k and the four distance metrics we defined above, then returns a tuple <tt>(k, distance_metric)</tt> representing the value of k and the distance metric that produce the best results with cross validation:
+ def find_best_k_and_metric(data):
- def branch_disorder(data, target_classifier):
+== Part 2E: More Multiple Choice ==
-For example, calling <tt>branch_disorder([ball3, ball4, ball5], ball_type_classifier)</tt> should yield approximately <tt>0.918</tt>.
+=== Questions 1-3: More tree classification ===
+These questions refer to the k-nearest neighbors data on classifying trees, from 2014 Quiz 2, Part B.
-Next, use your <tt>branch_disorder</tt> function to help compute the disorder of an entire test (a decision stump). Recall that the disorder of a test is the weighted average of the disorders of the constituent branches, where the weights are determined by the fraction of points in each branch.
+Recall the following terms:
+*Overfitting: Occurs when small amounts of noise in the training data are treated as meaningful trends in the population.  (i.e. when relying too heavily on the data, or overutilizing the data, causes a poor classification rate)
+*Underfitting: Occurs when the algorithm blurs out differences in the training data that reflect genuine trends in the population.  (i.e. when ignoring information in the data, or underutilizing the data, causes a poor classification rate)
-<tt>average_test_disorder</tt> should take in a list of points (the data), a Classifier (the feature test), and the <tt>target_classifier</tt> for determining the final classification of the points; it then computes and return the disorder of the entire test, as a number:
+'''kNN Question 1:''' Consider the results of cross-validation using k=1 and the Euclidean distance metric.  Why is 1 not a good value for k?  Answer "Overfitting" or "Underfitting" in kNN_ANSWER_1.
- def average_test_disorder(data, test_classifier, target_classifier):
+'''kNN Question 2:''' Consider the results of cross-validation using k=7 and the Euclidean distance metric.  Why is 7 not a good value for k?  Answer "Overfitting" or "Underfitting" in kNN_ANSWER_2.
-For example, calling <tt>average_test_disorder(ball_data, size_classifier, ball_type_classifier)</tt> should yield approximately <tt>0.959</tt>, because the "small" branch has weight <tt>3/5</tt> and a disorder of about <tt>0.918</tt>, while the "big" branch has a weight of <tt>2/5</tt> and a disorder of <tt>1</tt>.
+'''kNN Question 3:''' Euclidean distance doesn't seem to do very well with any value of k (for this data).  Which distance metric yields the highest classification rate for this dataset?  Answer 1, 2, 3, or 4 in kNN_ANSWER_3:
+#Euclidean distance
+#Manhattan distance
+#Hamming distance
+#Cosine distance
-=== Part 1D: Constructing an ID Tree ===
+=== Questions 4-7: Choosing metrics ===
-Using the disorder functions you defined above, implement a function to select the best classifier.  The function should take in some data (as a list of point dictionaries), a list of classifiers (<tt>Classifier</tt> objects), and the target classifier that you ultimately want your ID tree to be classifying by (e.g. a Classifier representing the test "Vampire?").  The function should return the classifier that has the lowest disorder.
+'''kNN Question 4:''' Suppose you wanted to classify a mysterious drink as coffee, energy drink, or soda based on the amount of caffeine and amount of sugar per 1-cup serving.  Coffee typically contains a large amount of caffeine, lemonade typically contains a large amount of sugar, and energy drinks typically contain a large amount of both.  Which distance metric would work best, and why?  Answer 1, 2, 3, or 4 in kNN_ANSWER_4:
+#Euclidean distance, because you're comparing standard numeric quantities
+#Manhattan distance, because it makes sense to array the training data points in a grid
+#Hamming distance, because the features "contains caffeine" and "contains sugar" are boolean values
+#Cosine distance, because you care more about the ratio of caffeine to sugar than the actual amount
-Edge cases:
+'''kNN Question 5:''' Suppose you add a fourth possible classification, water, which contains no caffeine or sugar.  Now which distance metric would work best, and why?  Answer 1, 2, 3, or 4 in kNN_ANSWER_5:
-* If multiple classifiers are tied for lowest disorder, break ties by preferring the classifier that occurs earlier in the list.
+#Euclidean distance, because you're still comparing standard numeric quantities, and it's now more difficult to compare ratios
-* If the classifier with lowest disorder wouldn't separate the data at all (that is, the classifier has only one branch), [[#How_to_handle_exceptions|raise the exception]] <tt>NoGoodClassifiersError</tt> instead of returning a classifier.
+#Manhattan distance, because there are now four points, so it makes even more sense to array them in a grid
+#Hamming distance, because the features "contains caffeine" and "contains sugar" are still boolean values
+#Cosine distance, because you still care more about the ratio of caffeine to sugar than the actual amount
-  def find_best_classifier(data, possible_classifiers, target_classifier):
+'''kNN Question 6:''' While visiting Manhattan, you discover that there are 3 different types of taxis, each of which has a distinctive logo.  Each type of taxi comes in many makes and models of cars.  Which distance metric would work best for classifying additional taxis based on their logos, makes, and models?  Answer 1, 2, 3, or 4 in kNN_ANSWER_6:
+#Euclidean distance, because there's a lot of variability in make and model
+#Manhattan distance, because the streets meet at right angles (and because you're in Manhattan and classifying taxicabs)
+#Hamming distance, because the features are non-numeric
+#Cosine distance, because it will separate taxis by how different their makes and models are
-Now, it is time to build an ID tree!
+'''kNN Question 7:''' Why might an ID tree work better for classifying the taxis from Question 6?  Answer 1, 2, 3, or 4 in kNN_ANSWER_7:
+#k-nearest neighbors requires data to be graphed on a coordinate system, but the training data isn't quantitative
+#Some taxis may have the same make and model, and k-nearest neighbors can't handle identical training points
+#An ID tree can ignore irrelevant features, such as make and model
+#Taxis aren't guaranteed to stay within their neighborhood in Manhattan
-The function <tt>construct_greedy_id_tree</tt> should take in four arguments:
-*<tt>data</tt>: a list of points
-*<tt>possible_classifiers</tt>: a list of Classifier objects that you can use in constructing your tree
-*<tt>target_classifier</tt>: the Classifier that the tree should ultimately classify by (e.g. a Classifier representing "Vampire?")
-*<tt>id_tree_node</tt> (optional): an incomplete tree, represented as an <tt>IdentificationTreeNode</tt>. If the incomplete tree is provided, finish it; if it is not provided, create a new tree using the constructor: <tt>id_tree_node = IdentificationTreeNode(target_classifier)</tt>
-Then, add classifiers and classifications to the tree until either perfect classification has been achieved, or there are no good classifiers left.
-We recommend implementing this function recursively (which can be done cleanly in about 15 lines). Your base case should occur when you encounter a leaf node, in which case you should set the node's classification.  The recursive step occurs when your classifier splits the data into groups, in which case you should set the classifier, expand the node (hint: <tt>set_classifier_and_expand</tt>), and recursively construct the tree for each new branch.
+For explanations of the answers to some of these questions, search for "#kNN_ANSWER_n" in tests.py, for the appropriate value of n.
-As a general outline:
+== Point API ==
-:1. Once the current id_tree_node is defined, perform one of three actions, depending on the input node's data and available classifiers:
-:* If the node is homogeneous, then it should be a leaf node, so add the classification to the node.
-:* If the node is not homogeneous and the data can be divided further, add the best classifier to the node.
-:* If the node is not homogeneous but there are no good classifiers left (i.e. no classifiers with more than one branch), leave the node's classification unassigned (which defaults to <tt>None</tt>).
-:2. If you added a classifier to the node, use recursion to complete each subtree.
-:3. Return the original input node.
- def construct_greedy_id_tree(data, possible_classifiers, target_classifier, id_tree_node=None):
+The <tt>Point</tt> class supports iteration (to iterate through the coordinates).
-Congrats, you're done constructing ID trees!
+A <tt>Point</tt> has the following attributes:
-We've provided some datasets from past quizzes, so you can now use your ID tree builder to solve problems!  For example, if you run
+;<tt>name</tt>
- print(construct_greedy_id_tree(tree_data, tree_classifiers, feature_test("tree_type")))
+:The name of the point (a string), if defined.
-...it should compute and print the solution to the tree-identification problem from 2014 Q2.
-You can also try:
+;<tt>coords</tt>
- print(construct_greedy_id_tree(angel_data, angel_classifiers, feature_test("Classification")))  #from 2012 Q2
+:The coordinates of the point, represented as a vector (a tuple or list of numbers).
- print(construct_greedy_id_tree(numeric_data, numeric_classifiers, feature_test("class")))  #from 2013 Q2
-You can also change the target_classifier attribute to, for example, use tree_type to predict what type of bark_texture a tree has:
+;<tt>classification</tt>
- print(construct_greedy_id_tree(tree_data, tree_classifiers_reverse, feature_test("bark_texture")))  #build an ID tree to predict bark_texture
+:The classification of the point, if known.
-==== Optional: Construct an ID tree with real medical data ====
-Constructing ID trees for small datasets (such as the ones from quiz problems) is straightforward and generally produces nice, simple trees.  But what happens if you construct an ID tree on a real-life dataset with hundreds of points and over a dozen features?  In a real medical situation, such as in an emergency room, doctors need a way to quickly determine which patients need immediate attention.  If a patient comes in complaining of chest pain, doctors may use an ID tree to ask the patient a series of medical questions to determine the likelihood that the patient has heart disease, or to distinguish between patients with heart disease, pneumonia, and broken ribs (all of which may cause chest pain, but require different treatments and different levels of urgency).
-We've provided a dataset [http://web.mit.edu/6.034/www/labs/lab5/cleveland_medical_data.txt cleveland_medical_data.txt] of anonymized medical data collected by the Cleveland Clinic Foundation.  The dataset contains information on 303 patients who were being checked for heart disease.  For each patient, it includes 13 features:
-* Age: int (in years)
-* Sex: M or F
-* Chest pain type: typical angina, atypical angina, non-anginal pain, or asymptomatic (Note that "angina" means "chest pain".)
-* Resting blood pressure: int (in mm Hg)
-* Cholesterol level: int (in mg/dl)
-* Is fasting blood sugar < 120 mg/dl: Yes or No
-* Resting EKG type: normal, wave abnormality, or ventricular hypertrophy
-* Maximum heart rate: int
-* Does exercise cause chest pain?: Yes or No
-* ST depression induced by exercise: int
-* Slope type: up, flat, or down
-* # of vessels colored: float or '?' (This is the number of major vessels (0-3) colored by flourosopy.)
-* Thal type: normal, fixed defect, reversible defect, or unknown
-(If you don't understand all the medical terminology, don't worry -- you can still use the data!)
-Each patient also has a known classification, represented both on a binary scale and on a discrete scale:
-* Heart disease presence: healthy or diseased
-* Heart disease level: int 0-4, where 0 means healthy (no presence of heart disease), and 1-4 indicate different levels of heart disease, with 4 being the most severe
-In parse.py, we've parsed the dataset for you and stored it in the variable <tt>heart_training_data</tt>.  <tt>heart_training_data</tt> is a list of 303 dictionaries, where each dictionary represents a patient and looks something like this:
-<tt>{'name': 'patient280', 'Cholesterol level': 282, 'ST depression induced by exercise': 1, 'Age': 65, 'Resting EKG type': 'ventricular hypertrophy', 'Chest pain type': 'typical angina', 'Does exercise cause chest pain?': 'No', 'Sex': 'M', 'Thal type': 'normal', '# of vessels colored': 1.0, 'Is fasting blood sugar < 120 mg/dl': 'Yes', 'Resting blood pressure': 138, 'Maximum heart rate': 174, 'Heart disease level': 1, 'Slope type': 'flat', 'Heart disease presence': 'diseased'}</tt>
-We've also defined a list of 345 Classifiers, most of which are numeric threshold classifiers.  As recommended in lecture, we included a threshold classifier between every pair of neighboring possible values for a feature.  For example, if one patient has a cholesterol level of 150 and another has 156, but there are no values in between, we'll add a Classifier for "Cholesterol level > 153".  All of the classifiers are stored in the variable <tt>heart_classifiers</tt>.
-Finally, we've defined two possible target classifiers:
-* <tt>heart_target_classifier_binary</tt>, for the binary "Heart disease presence", and
-* <tt>heart_target_classifier_discrete</tt>, for the discrete "Heart disease level".
-'''To construct an ID tree with this dataset''', all you need to do is add <tt>from parse import *</tt> to your lab5.py file, then call <tt>construct_greedy_id_tree</tt> with the heart data, heart classifiers, and target classifier of your choice.
-What do you notice?  Does this seem like the simplest possible tree? If not, why not? What could we change to make it simpler?
-Try using the other target classifier (binary or discrete). Is the tree simpler or more complicated? Why?
-Try using <tt>tree.print_with_data</tt> to print the training data at the leaf nodes. What do you notice?
-'''To diagnose a new patient''', first create a dictionary of their attributes, for example:
-<pre>
-test_patient = {\
-    'Age': 20, #int
-    'Sex': 'F', #M or F
-    'Chest pain type': 'asymptomatic', #typical angina, atypical angina, non-anginal pain, or asymptomatic
-    'Resting blood pressure': 100, #int
-    'Cholesterol level': 120, #int
-    'Is fasting blood sugar < 120 mg/dl': 'Yes', #Yes or No
-    'Resting EKG type': 'normal', #normal, wave abnormality, or ventricular hypertrophy
-    'Maximum heart rate': 150, #int
-    'Does exercise cause chest pain?': 'No', #Yes or No
-    'ST depression induced by exercise': 0, #int
-    'Slope type': 'flat', #up, flat, or down
-    '# of vessels colored': 0, #float or '?'
-    'Thal type': 'normal', #normal, fixed defect, reversible defect, or unknown
-}
-</pre>
-Then use your <tt>id_tree_classify_point</tt> function or <tt>tree.print_with_data([test_patient])</tt> to classify the patient.
-If you get an error such as <tt>KeyError: '?'</tt> when using <tt>id_tree_classify_point</tt>, it's not a bug in your code; it just means that the ID tree is unable to classify the point.  Either define a different patient, or use <tt>tree.print_with_data</tt> to see why the point is unclassifiable.
-;Important Legal Disclaimer
-:Please do not use this to perform real medical diagnosis.  As the questions below will show, there are numerous factors that may cause your ID tree to mis-classify patients.
-Try creating and classifying a few patients. (You can copy/paste the <tt>test_patient</tt> code into your <tt>lab5.py</tt> file to define your own patients.) Are the results consistent with your expectations?
-What happens if a female patient has <tt>'Thal type': 'unknown'</tt>?  What happens if a male patient has <tt>'Thal type': 'unknown'</tt>? If you're surprised by the results, examine your tree and data to figure out what caused the results. (You can use <tt>tree.print_with_data</tt> to print your tree with all the training points.)  What could we change to improve the classification accuracy of patients with unknown Thal type?
-In the discrete classification tree, what happens if a patient has <tt>'Thal type': 'normal'</tt>, <tt>'Chest pain type': 'asymptomatic'</tt>, and <tt>'# of vessels colored': '?'</tt>?  Why does this happen?  Why might it cause a problem for classifying real patients?  What can we do to fix this problem?
-(For answers to the questions in this section, look at the bottom of <tt>parse.py</tt>.)
-=== Part 1E: Multiple Choice ===
-==== Questions 1-3: Identification (of) Trees ====
-These questions refer to the data from 2014 Quiz 2, Problem 1, Part A, which is stored in the variables <tt>tree_data</tt> (the data) and <tt>tree_classifiers</tt> (a list of Classifiers) in <tt>data.py</tt>.
-'''Question 1:''' Which of the four classifiers (a.k.a. feature tests) has the lowest disorder?  Fill in ANSWER_1 with one of the four classifiers as a string: 'has_leaves', 'leaf_shape', 'orange_foliage', or 'bark_texture'.  <!--If multiple classifiers are tied for having the lowest disorder, instead fill in ANSWER_1 with a list of classifier names.-->
-'''Question 2:''' Which of the four classifiers has the ''second'' lowest disorder?  Fill in ANSWER_2 with one of the four classifiers as a string.
-'''Question 3:''' If we start constructing the greedy, disorder-minimizing ID tree, we'll start with the classifier from Question 1.  Our one-classifier tree has exactly one non-homogeneous branch.  For that branch, which of the four classifiers has the lowest disorder?  Fill in ANSWER_3 with one of the four classifiers as a string.
-==== Questions 4-7: XOR ====
-Each training point in the dataset below has three binary features (A, B, C) and a binary classification (0 or 1).  Note that the classification happens to be the boolean function XOR(A,B), while feature C is just random noise.  The dataset is available in <tt>data.py</tt> as <tt>binary_data</tt>, and the three classifiers are stored in the variable <tt>binary_classifiers</tt>.
-{| cellpadding=5 border=1 cellspacing=0 style="text-align: center;"
-|- bgcolor=#eeeeee
-! Classification !! A !! B !! C
-|-
-| 0 || 0 || 0 || 0
-|-
-| 0 || 0 || 0 || 1
-|-
-| 1 || 0 || 1 || 0
-|-
-| 1 || 0 || 1 || 1
-|-
-| 1 || 1 || 0 || 1
-|-
-| 1 || 1 || 0 || 1
-|-
-| 0 || 1 || 1 || 0
-|}
-Consider the three identification trees below.  They are defined in the lab code as <tt>binary_tree_n</tt>, for <tt>n</tt> from 1 to 3.  To answer the questions below, you may use your code or work out the answers by hand.
-[[Image:Lab5_binary_trees.png]]
-'''Question 4''': Which of the trees correctly classify all of the training data?  Fill in ANSWER_4 with a list of numbers (e.g. <tt>[1,2]</tt> if trees 1 and 2 correctly classify the training data but tree 3 does not, or <tt>[]</tt> if no tree correctly classifies the training data).
-'''Question 5''': Which of the trees could be created by the greedy, disorder-minimizing ID tree algorithm?  Fill in ANSWER_5 with a list of numbers.
-'''Question 6''': For ''any'' binary dataset with features A, B, and C, which trees correctly compute the function Classification=XOR(A,B)?  Fill in ANSWER_6 with a list of numbers.
-'''Question 7''': Based on the principle of Occam's Razor, which tree (among the ones that correctly classify the data) is likely to give the most accurate results when classifying unknown test points?  Fill in ANSWER_7 with a single number, as an int.
-==== Questions 8-9: General properties of greedy ID trees ====
-These questions are about ID trees in general and do not refer to any specific trees, data, or classifiers.
-'''Question 8:''' When constructing an ID tree, in the first round we pick a classifier for the top node, in the second round we pick classifiers for the children nodes, and so on. With this in mind, when constructing a greedy, disorder-minimizing ID tree, is the classifier with the ''second'' lowest disorder in the first round always the same as the classifier with the ''lowest'' disorder in the second round?  (Hint: Consider your answers to Questions 1-3.)  Answer 'Yes' or 'No' in ANSWER_8.
-'''Question 9''': Will a greedy, disorder-minimizing tree always be the simplest possible tree to correctly classify the data?  (Hint: Consider your answers to Questions 4-7.)  Answer 'Yes' or 'No' in ANSWER_9.
-For explanations of the answers to these questions, search for "#ANSWER_n" in tests.py, for the appropriate value of n.
-== Point API ==
-The <tt>Point</tt> class supports iteration (to iterate through the coordinates).
-A <tt>Point</tt> has the following attributes:
-*<b><tt>point</tt></b><tt>.name</tt>, the name of the point (a string), if defined.
-*<b><tt>point</tt></b><tt>.coords</tt>, the coordinates of the point, represented as a vector (a tuple or list of numbers).
-*<b><tt>point</tt></b><tt>.classification</tt>, the classification of the point, if known.